
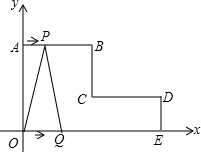
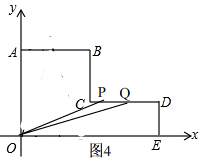
 ��ͼ����ƽ��ֱ������ϵ�У�AB��CD��x�ᣬBC��DE��y�ᣬ��AB=CD=4��OA=4��DE=2������P�ӵ�A��������A��B��C·���˶�����Cֹͣ������Q�ӵ�O��������O��E��D��C·���˶�����Cֹͣ����P��Q����ͬʱ�������ҵ�P���˶��ٶ�Ϊÿ��1����λ����Q���˶��ٶ�Ϊÿ��2����λ��
��ͼ����ƽ��ֱ������ϵ�У�AB��CD��x�ᣬBC��DE��y�ᣬ��AB=CD=4��OA=4��DE=2������P�ӵ�A��������A��B��C·���˶�����Cֹͣ������Q�ӵ�O��������O��E��D��C·���˶�����Cֹͣ����P��Q����ͬʱ�������ҵ�P���˶��ٶ�Ϊÿ��1����λ����Q���˶��ٶ�Ϊÿ��2����λ������ ��1���������P��Q�����꣬�����CP��CQ��Ȼ����������ε������ʽ��ʽ���㼴�ɵý⣻
��2���֢�0��t��4ʱ��P��AB�ϣ���Q��OE�ϣ����������������ʽ��ʽ���ɣ�
��4��t��5ʱ����P��BC�ϣ���Q��DE�ϣ�����P��PM��CD��DE���ӳ�����M������S��OPQ=S����OPMB-S��PMQ-S��OEQ����ʽ�������ɣ�
��5��t��6ʱ����P��BC�ϣ���Q��CD�ϣ�����P��PF��CD������Q��QF��OA��PF��F����OE��G��S��OPQ=S����OPFG-S��PFQ-S��OGQ����ʽ�������ɵý⣬
��6��t��$\frac{20}{3}$ʱ����P��Q����CD�ϣ�ֱ���������ε������ʽ���ɣ�
��3���������������M�����꣬���õ��������ε�����ֱ�������OBM��
��� ��1����t=$\frac{11}{2}$sʱ����P�˶���·��Ϊ$\frac{11}{2}$��
��Q�˶���·��Ϊ$\frac{11}{2}$��2=11��
���ԣ�P��4��$\frac{5}{2}$����Q��7��2����
��CP=$\frac{1}{2}$��CQ=3��
��S��CPQ=$\frac{1}{2}$CP•CQ=$\frac{1}{2}$��$\frac{1}{2}$��3=$\frac{3}{4}$��
��2��������ã�
��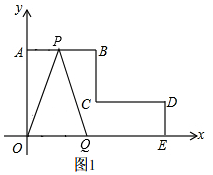
��0��t��4ʱ������ͼ1��OA=4��OQ=2t��
S��OPQ=$\frac{1}{2}$OQ•OA=$\frac{1}{2}$��2t��4=4t��
��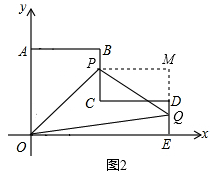
��4��t��5ʱ������ͼ2��OE=8��EM=8-t��PM=4��MQ=16-3t��EQ=2t-8��
S��OPQ=S����OPMB-S��PMQ-S��OEQ��
=$\frac{1}{2}$��4+8������8-t��-$\frac{1}{2}$��4����16-3t��-$\frac{1}{2}$��8��2t-8����
=48-8t��
��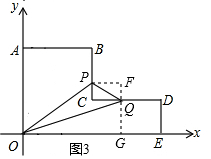
��5��t��6ʱ������ͼ3��PF=14-2t��FQ=7-t��QG=2��OG=18-2t��FG=8-t��
S��OPQ=S����OPFG-S��PFQ-S��OGQ��
=$\frac{1}{2}$����14-2t+18-2t������8-t��-$\frac{1}{2}$����14-2t����7-t��-$\frac{1}{2}$��18-2t����2��
=t2-16t+61��
��
��6��t��$\frac{20}{3}$ʱ����ͼ4��PQ=20-3t��DE=2��
S��OPQ=$\frac{1}{2}$PQ��DE=$\frac{1}{2}$��20-3t����2=20-3t
����������S=$\left\{\begin{array}{l}{4t��0��t��4��}\\{48-8t��4��t��5��}\\{{t}^{2}-16t+61��5��t��6��}\\{20-3t��6��t��\frac{20}{3}��}\end{array}\right.$��
��3����ͼ��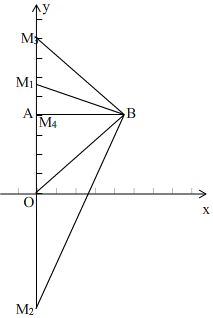
������õ�B��4��4����
��OB=4$\sqrt{2}$��
���M��0��m����
��OM=|m|��BM=$\sqrt{��m-4��^{2}+16}$��
����O��B��M����Ϊ������������ǵ��������Σ�
��ٵ�OB=OMʱ��
��|m|=4$\sqrt{2}$��
��m=4$\sqrt{2}$��m=-4$\sqrt{2}$��
��m=4$\sqrt{2}$ʱ��M1��0��4$\sqrt{2}$����
���OBM1=$\frac{180��-45��}{2}$=67.5�㣬
��m=-4$\sqrt{2}$ʱ��M2��0��-4$\sqrt{2}$����
���OBM2=$\frac{��AOB}{2}$=$\frac{45��}{2}$=22.5��
�ڵ�OB=PMʱ��
��4$\sqrt{2}$=$\sqrt{��m-4��^{2}+16}$��
��m=0���ᣩ��m=8��
��M3��0��8����
���BM3O=��BOM3=45�㣬
���OBM3=90��
�۵�OM=PMʱ��
��|m|=$\sqrt{��m-4��^{2}+16}$��
��m=4��
��M4��0��4������ʱ��M4�͵�A�غϣ�
���OBM4=��OBA=45�㣮
���� �������������ۺ��⣬��Ҫ������������ͼ�����ʣ������ε������ƽ���ߵ����ʣ����������ε����ʺ��ж����ѵ����ڣ�3�����ݵ�P��Q��λ�ã���������ۣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | �ı��ε���Ǻ͵����ڽǺ� | |
| B�� | ���еľ��ζ����� | |
| C�� | �Խ�����ȵ������������� | |
| D�� | �Խ����ഹֱ��ƽ���ı��������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 30�� | B�� | 15�� | C�� | 45�� | D�� | 60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
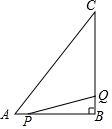 ��ͼ���ڡ�ABC�У���B=90�㣬AB=6cm��BC=8cm����P�ӵ�A��ʼ��AB�����B��1cm/s���ٶ��ƶ�����Q�ӵ�B��ʼ��BC�����C��2cm/s���ٶ��ƶ�����P��Q����ͬʱ����������Q�˶�����Cʱ��P��Q����ͬʱֹͣ�˶������������˶�������PQ�ij��ȱ仯����ǣ�������
��ͼ���ڡ�ABC�У���B=90�㣬AB=6cm��BC=8cm����P�ӵ�A��ʼ��AB�����B��1cm/s���ٶ��ƶ�����Q�ӵ�B��ʼ��BC�����C��2cm/s���ٶ��ƶ�����P��Q����ͬʱ����������Q�˶�����Cʱ��P��Q����ͬʱֹͣ�˶������������˶�������PQ�ij��ȱ仯����ǣ�������| A�� | �ȱ䳤���� | B�� | һֱ��� | C�� | һֱ�䳤 | D�� | �ȱ�̺�䳤 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
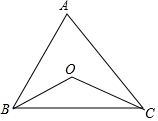 ��ͼ����ABC�У���ABC���ACB�Ľ�ƽ���߽��ڵ�O������BAC=82�㣬���BOC=131����
��ͼ����ABC�У���ABC���ACB�Ľ�ƽ���߽��ڵ�O������BAC=82�㣬���BOC=131�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
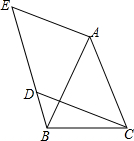 AB���ı���ACBE�ĶԽ��ߣ�AB=AC������C��CD��AE��BE��D����AE=DE����ACD=45�㣬BD=1��CD=5����AE=$\frac{13}{4}$��
AB���ı���ACBE�ĶԽ��ߣ�AB=AC������C��CD��AE��BE��D����AE=DE����ACD=45�㣬BD=1��CD=5����AE=$\frac{13}{4}$���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com