
����Ŀ���������
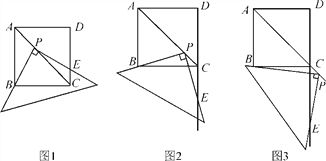
(1)��ͼ1����ֱ�����ǰ��ֱ�Ƕ���P����������ABCD�ĶԽ���AC�ϣ�һ��ֱ�DZ߾�����B����һ��ֱ�DZ߽���DC�ڵ�E���߶�PB���߶�PE�������֤����
����̽��
(2)��ͼ2���ƶ����ǰ壬ʹ���ǰ��ֱ�Ƕ���P�ڶԽ���AC�ϣ�һ��ֱ�DZ߾�����B����һ��ֱ�DZ߽�DC���ӳ����ڵ�E��(1)�еĽ��ۻ�����������������֤����������������˵�����ɣ�
������
(3)�����ƶ����ǰ壬ʹ���ǰ��ֱ�Ƕ���P�ڶԽ���AC�ϣ�һ��ֱ�DZ߾�����B����һ��ֱ�DZ߽�DC���ӳ����ڵ�E��(1)�еĽ��ۻ�����������������֤����������������˵�����ɣ�
��
���𰸡���1��֤����������2��PB��PE������(3) PB��PE������
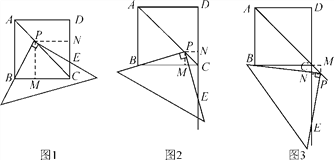
�������������������1�����������ε����ʵá�BCD=90�㣬ACƽ�֡�BCD����PM��CD�����ı���PMCN�Ǿ��Σ����ݽ�ƽ���ߵ����ʿɵ�PM=PN�������ı��ε��ڽǺ͵õ���PBC+��CEP=180�㣬�����õȽǵIJ�����ȵõ���PBM=��PEN��Ȼ�����AAS֤����PBM�ա�PEN�����֤����
��2������PD�����������ε����ʺͽ�ƽ���ߵ����ʣ��ɡ�SAS���Լ��ı��ε��ڽǺ͵�֤��
��3������P��PM��BC��PN��CD��Ȼ����ݽ�ƽ���ߵ����ʺ������ε����ʣ��ɡ�AAS����֤.
���������(1)��ͼ1������P��PM��BC��PN��CD������ֱ�ΪM��N�����ı���ABCDΪ�����Σ����BCD��90�㣬ACƽ����BCD����PM��BC��PN��CD�����ı���PMCNΪ�����Σ�PM��PN���ߡ�BPE��90�㣬��BCD��90�㣬���PBC����CEP��180��������CEP����PEN��180�㣬���PBM����PEN������PBM����PEN�У� 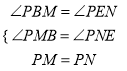 ���PBM�ա�PEN(AAS)����PB��PE��(2)��ͼ2��PB��PE���������������£�����P��PM��BC��PN��CD������ֱ�ΪM��N�����ı���ABCDΪ�����Σ����BCD��90�㣬ACƽ����BCD����PM��BC��PN��CD�����ı���PMCNΪ�����Σ�PM��PN�����MPN��90�㣬�ߡ�BPE��90�㣬��BCD��90�㣬���BPM����MPE��90��������MPE����EPN��90�㣬���BPM����EPN������PBM����PEN�У�
���PBM�ա�PEN(AAS)����PB��PE��(2)��ͼ2��PB��PE���������������£�����P��PM��BC��PN��CD������ֱ�ΪM��N�����ı���ABCDΪ�����Σ����BCD��90�㣬ACƽ����BCD����PM��BC��PN��CD�����ı���PMCNΪ�����Σ�PM��PN�����MPN��90�㣬�ߡ�BPE��90�㣬��BCD��90�㣬���BPM����MPE��90��������MPE����EPN��90�㣬���BPM����EPN������PBM����PEN�У� 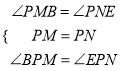 ���PBM�ա�PEN(ASA)����PB��PE��(3)��ͼ3��PB��PE���������������£�����P��PM��BC��BC���ӳ����ڵ�M��PN��CD���ӳ����ڵ�N�����ı���ABCDΪ�����Σ����BCD��90�㣬ACƽ����BCD����PM��BC��PN��CD�����ı���PMCNΪ�����Σ�PM��PN�����MPN��90�㣬�ߡ�BPE��90�㣬��BCD��90�㣬���BPM����BPN��90��������BPN����EPN��90�㣬���BPM����EPN������PBM����PEN�У�
���PBM�ա�PEN(ASA)����PB��PE��(3)��ͼ3��PB��PE���������������£�����P��PM��BC��BC���ӳ����ڵ�M��PN��CD���ӳ����ڵ�N�����ı���ABCDΪ�����Σ����BCD��90�㣬ACƽ����BCD����PM��BC��PN��CD�����ı���PMCNΪ�����Σ�PM��PN�����MPN��90�㣬�ߡ�BPE��90�㣬��BCD��90�㣬���BPM����BPN��90��������BPN����EPN��90�㣬���BPM����EPN������PBM����PEN�У�  ���PBM�ա�PEN(ASA)����PB��PE
���PBM�ա�PEN(ASA)����PB��PE


 �����Ƹ���ʦ����ϵ�д�
�����Ƹ���ʦ����ϵ�д� ��ͨ����ͬ����ϰ��ϵ�д�
��ͨ����ͬ����ϰ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A.x3x2��x6B.����x2��4��x6C.x6��x5��xD.x2+x3��x5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������������һ��������ӯ�������������⣬ԭ�����£������˹�����˳��ˣ�ӯ�����˳��ߣ������ģ����������Σ�����Ϊ������һЩ�˹�ͬ��һ����Ʒ��ÿ�˳�8Ԫ����ӯ��3Ԫ��ÿ�˳�7Ԫ����4Ԫ���ʹ���_____�ˣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ʽ������ȫƽ��ʽ���ǣ�������
A.a2+2ab��b2B.a2+2a+1C.a2+ab+b2D.a2+2a��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
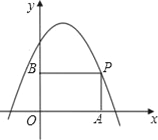
����Ŀ����ͼ��P��������y=��x2+x+2�ڵ�һ�����ϵĵ㣬����P�ֱ���x���y�������ߣ�����ֱ�ΪA��B�����ı���OAPB�ܳ������ֵΪ_____��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����6��6�������������У�ÿ��С�����εı߳���Ϊ1���������������а�����Ҫ��ͼ�Σ�

��1���ӵ�A������һ���߶�AB��ʹ������һ���˵����ڸ�㣨��С�����εĶ��㣩�ϣ��ҳ���Ϊ![]() ��
��
��2���ԣ�1���е�ABΪ�ߵ�һ������������ABC��ʹ��C�ڸ���ϣ��뻭���������������ĵ�C��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��Ϊ�˽�����ѧУ�����˶����б���ͻ����ͬѧ��������������ίԱС�����ľߵ�Ϊ��ͬѧ��Ʒ��С�����֣������1���ʼDZ���3֧�ֱʣ�����Ҫ19Ԫ�������2���ʼDZ���5֧�ֱʣ�����Ҫ33Ԫ��
��1������ÿ���ʼDZ���ÿ֧�ֱʸ�����Ԫ��
��2�������θ�С���İ��ֻ��110Ԫ��Ҫ����24��ͬѧÿ��һ����Ʒ����С������Ҫ������ٱ��ʼDZ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����ABCD�У�AB=6��BC=8
��1����Խ���AC�ij���
��2����E���߶�CD�ϵ�һ�㣬�ѡ�ADE����ֱ��AE�۵�����Dǡ�������߶�AC�ϣ���F�غϣ����߶�DE�ij��� 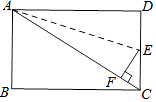
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com