
【题目】已知抛物线C1:y=ax2﹣4ax﹣5(a>0). 
(1)当a=1时,求抛物线与x轴的交点坐标及对称轴;
(2)①试说明无论a为何值,抛物线C1一定经过两个定点,并求出这两个定点的坐标;②将抛物线C1沿这两个定点所在直线翻折,得到抛物线C2 , 直接写出C2的表达式;
(3)若(2)中抛物线C2的顶点到x轴的距离为2,求a的值.
【答案】
(1)解:当a=1时,抛物线解析式为y=x2﹣4x﹣5=(x﹣2)2﹣9,
∴对称轴为y=2;
∴当y=0时,x﹣2=3或﹣3,即x=﹣1或5;
∴抛物线与x轴的交点坐标为(﹣1,0)或(5,0)
(2)解:①抛物线C1解析式为:y=ax2﹣4ax﹣5,
整理得:y=ax(x﹣4)﹣5;
∵当ax(x﹣4)=0时,y恒定为﹣5;
∴抛物线C1一定经过两个定点(0,﹣5),(4,﹣5);
②这两个点连线为y=﹣5;
将抛物线C1沿y=﹣5翻折,得到抛物线C2,开口方向变了,但是对称轴没变;
∴抛物线C2解析式为:y=﹣ax2+4ax﹣5
(3)解:抛物线C2的顶点到x轴的距离为2,
则x=2时,y=2或者﹣2;
当y=2时,2=﹣4a+8a﹣5,解得,a= ![]() ;
;
当y=﹣2时,﹣2=﹣4a+8a﹣5,解得,a= ![]() ;
;
∴a= ![]() 或
或 ![]()
【解析】(1)将a=1代入解析式,即可求得抛物线与x轴交点;(2)①化简抛物线解析式,即可求得两个点定点的横坐标,即可解题;②根据抛物线翻折理论即可解题;(3)根据(2)中抛物线C2解析式,分类讨论y=2或﹣2,即可解题;
【考点精析】关于本题考查的二次函数图象的平移和抛物线与坐标轴的交点,需要了解平移步骤:(1)配方 y=a(x-h)2+k,确定顶点(h,k)(2)对x轴左加右减;对y轴上加下减;一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.才能得出正确答案.


科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象与x轴交于A,B两点,其中点A(﹣1,0),点C(0,5),点D(1,8)都在抛物线上,M为抛物线的顶点. 
(1)求抛物线的函数解析式;
(2)求△MCB的面积;
(3)根据图形直接写出使一次函数值大于二次函数值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两列火车分别从A,B两城同时相向匀速驶出,甲车开往终点B城,乙车开往终点A城,乙车比甲车早到达终点;如图所示,是两车相距的路程d(千米)与行驶时间t(小时)的函数的图象. 
(1)经过小时两车相遇;
(2)A,B两城相距千米路程;
(3)分别求出甲、乙两车的速度;
(4)分别求出甲车距A城的路程s甲、乙车距A城的路程s乙与t的函数关系式;(不必写出t的范围)
(5)当两车相距200千米路程时,求t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过 ![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE. 
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG= ![]() ,AH=3
,AH=3 ![]() ,求EM的值.
,求EM的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,研究发现,科学使用电脑时,望向荧光屏幕画面的“视线角”α约为20°,而当手指接触键盘时,肘部形成的“手肘角”β约为100°.图2是其侧面简化示意图,其中视线AB水平,且与屏幕BC垂直. 
(1)若屏幕上下宽BC=20cm,科学使用电脑时,求眼睛与屏幕的最短距离AB的长;
(2)若肩膀到水平地面的距离DG=100cm,上臂DE=30cm,下臂EF水平放置在键盘上,其到地面的距离FH=72cm.请判断此时β是否符合科学要求的100°? (参考数据:sin69°≈ ![]() ,cos21°≈
,cos21°≈ ![]() ,tan20°≈
,tan20°≈ ![]() ,tan43°≈
,tan43°≈ ![]() ,所有结果精确到个位)
,所有结果精确到个位)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,O是对角线AC与BD的交点,M是BC边上的动点(点M不与B,C重合),CN⊥DM,CN与AB交于点N,连接OM,ON,MN.下列五个结论:①△CNB≌△DMC;②△CON≌△DOM;③△OMN∽△OAD;④AN2+CM2=MN2;⑤若AB=2,则S△OMN的最小值是 ![]() ,其中正确结论的个数是( )
,其中正确结论的个数是( ) 
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,在Rt△ABC中,∠ACB=90°,AC=4,BC=2,D是AC边上的一个动点,将△ABD沿BD所在直线折叠,使点A落在点P处.
(1)如图1,若点D是AC中点,连接PC.
①写出BP,BD的长;
②求证:四边形BCPD是平行四边形.
(2)如图2,若BD=AD,过点P作PH⊥BC交BC的延长线于点H,求PH的长.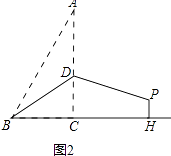
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等边△ABC中,点E、D分别是AC,BC边的中点,点P为AB边上的一个动点,连接PE,PD,PC,DE.设AP=x,图1中某条线段的长为y,若表示y与x的函数关系的图象大致如图2所示,则这条线段可能是图1中的( )
A.线段DE
B.线段PD
C.线段PC
D.线段PE
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小宇想测量位于池塘两端的A、B两点的距离.他沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到点D处,测得∠BDF=60°.若直线AB与EF之间的距离为60米,求A、B两点的距离. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com