
【题目】已知,如图,在![]() 中,
中,![]() ,点
,点![]() 在
在![]() 上,
上,![]() ,点
,点![]() 在
在![]() 上,连接
上,连接![]() 、
、![]() .
.
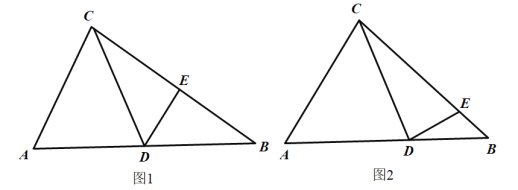
(1)如图1,若![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的长.
的长.
(2)如图2,若![]() ,且
,且![]() ,求证:
,求证:![]() .
.
科目:初中数学 来源: 题型:
【题目】甲、乙、丙、丁4名同学进行一次羽毛球单打比赛,要从中选2名同学打第一场比赛,求下列事件的概率。
(1)已确定甲打第一场,再从其余3名同学中随机选取1名,恰好选中乙同学;
(2)随机选取2名同学,其中有乙同学.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车销售公司经销某品牌![]() 款汽车,随着汽车的普及,其价格也在不断下降.今年5月份
款汽车,随着汽车的普及,其价格也在不断下降.今年5月份![]() 款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的
款汽车的售价比去年同期每辆降价1万元,如果卖出相同数量的![]() 款汽车,去年销售额为100万元,今年销售额只有90万元.
款汽车,去年销售额为100万元,今年销售额只有90万元.
(1)今年5月份![]() 款汽车每辆售价多少万元?
款汽车每辆售价多少万元?
(2)为了增加收入,汽车销售公司决定再经销同品牌的![]() 款汽车,已知
款汽车,已知![]() 款汽车每辆进价为7.5万元,
款汽车每辆进价为7.5万元,![]() 款汽车每辆进价为6万元,公司预计用不多于105万元且不少于102万元的资金购进这两款汽车共15辆,有几种进货方案?
款汽车每辆进价为6万元,公司预计用不多于105万元且不少于102万元的资金购进这两款汽车共15辆,有几种进货方案?
(3)按照(2)中两种汽车进价不变,如果![]() 款汽车每辆售价为8万元,为打开
款汽车每辆售价为8万元,为打开![]() 款汽车的销路,公司决定每售出一辆
款汽车的销路,公司决定每售出一辆![]() 款汽车,返还顾客现金
款汽车,返还顾客现金![]() 万元,要使(2)中所有的方案获利相同,
万元,要使(2)中所有的方案获利相同,![]() 值应是多少?
值应是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
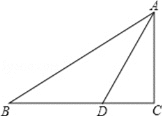
【题目】已知:如图,在 Rt△ABC 中,∠C=90°,∠B=30°,AD 平分∠BAC.
(1)求证:点 D 在 AB 的垂直平分线上;
(2)若 CD=2,求 BC 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
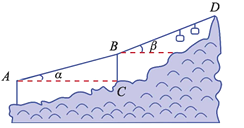
【题目】缆车,不仅提高了景点接待游客的能力,而且解决了登山困难者的难题.如图,当缆车经过点A到达点B时,它走过了700米.由B到达山顶D时,它又走过了700米.已知线路AB与水平线的夹角![]() 为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
为16°,线路BD与水平线的夹角β为20°,点A的海拔是126米.求山顶D的海拔高度(画出设计图,写出解题思路即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将某点(横坐标与纵坐标不相等)的横坐标与纵坐标互换后得到的点叫这个点的“互换点”,如(-3,5)与(5,-3)是一对“互换点”.
(1)以O为圆心,半径为5的圆上有无数对“互换点”,请写出一对符合条件的“互换点”;
(2)点M,N是一对“互换点”,点M的坐标为(m,n),且(m>n),⊙P经过点M,N.
①点M的坐标为(4,0),求圆心P所在直线的表达式;
②⊙P的半径为5,求m-n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校选学生会正副主席,需要从甲班的2名男生1名女生(男生用A,B表示,女生用a表示)和乙班的1名男生1名女生(男生用C表示,女生用b表示)共5人中随机选出2名同学.
(1)用树状图或列表法列出所有可能情形;
(2)求2名同学来自不同班级的概率;
(3)求2名同学恰好1男1女的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,AB=3,AD=4,动点Q从点A出发,以每秒1个单位的速度,沿AB向点B移动;同时点P从点B出发,仍以每秒1个单位的速度,沿BC向点C移动,连接QP,QD,PD.若两个点同时运动的时间为x秒(0<x≤3),解答下列问题:
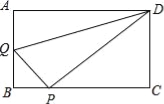

(1)设△QPD的面积为S,用含x的函数关系式表示S;当x为何值时,S有最大值?并求出最小值;
(2)是否存在x的值,使得QP⊥DP?试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点O为坐标原点,抛物线y=-![]() x2+bx+c交x轴于A、B两点,交y轴于点C,直线y=x+6经过A、C两点.
x2+bx+c交x轴于A、B两点,交y轴于点C,直线y=x+6经过A、C两点.
(1)求抛物线的解析式;
(2)点P是第二象限抛物线上的一个动点,过点P作PQ∥AC,PQ交直线BC于点Q,设点P的横坐标为t,点Q的横坐标为m,求m与t之间的函数关系式(不要求写出自变量t的取值范围);
(3)在(2)的条件下,作点P关于直线AC的对称点点K,连接QK,当点K落在直线y=-![]() x上时,求线段QK的长.
x上时,求线段QK的长.



查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com