
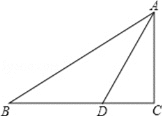
【题目】已知:如图,在 Rt△ABC 中,∠C=90°,∠B=30°,AD 平分∠BAC.
(1)求证:点 D 在 AB 的垂直平分线上;
(2)若 CD=2,求 BC 的长.
【答案】(1)证明见解析;(2)6
【解析】
(1)先根据三角形内角和定理得∠BAC=60°,再根据AD 平分∠BAC,可得∠BAD=∠B=30°,即AD=BD,得证点D在AB的垂直平分线上;
(2)根据特殊三角函数值求得AD=2CD=4,结合(1)得BD=AD=4,即可求出BC 的长.
(1)在Rt△ABC中,∠C=90°,∠B=30°,
∴∠BAC=60°.
又∵AD平分∠BAC,
∠BAD=∠CAD=30°
∴∠BAD=∠B=30°,
∴AD=BD
∴点D在AB的垂直平分线上
(2)∵AD=BD,∠B=30°
∴![]()
∴![]()
在Rt△ACD中,∠C=90°,![]()
∴AD=2CD=4
由(1)得BD=AD=4
∴BC=BD+CD=2+4=6


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E、F,连结BD、DP,BD与CF相交于点H.给出下列结论:
①△BDE∽△DPE;②![]() =
=![]() ;③DP2=PHPB;④tan∠DBE=2﹣
;③DP2=PHPB;④tan∠DBE=2﹣![]() .
.
其中正确的是( )
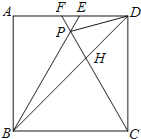
A.①②③④ B.①②④ C.②③④ D.①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(﹣6,0),B(4,0),C(0,8),把△ABC沿直线BC翻折,点A的对应点为D,抛物线y=ax2﹣10ax+c经过点C,顶点M在直线BC上.

(1)证明四边形ABCD是菱形,并求点D的坐标;
(2)求抛物线的对称轴和函数表达式;
(3)在抛物线上是否存在点P,使得△PBD与△PCD的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
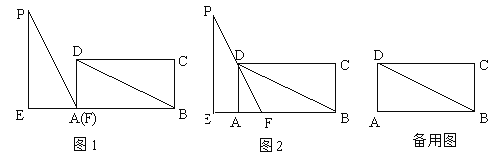
【题目】如图1,在矩形ABCD中,DB=6,AD=3,在Rt△PEF中,∠PEF=90°,EF=3,PF=6,△PEF(点F和点A重合)的边EF和矩形的边AB在同一直线上.现将Rt△PEF从A以每秒1个单位的速度向射线AB方向匀速平移,当点F与点B重合时停止运动,设运动时间为t秒,
解答下列问题:
(1)如图1,连接PD,填空:∠PFD= ,四边形PEAD的面积是 ;
(2)如图2,当PF经过点D时,求 △PEF运动时间t的值;
(3)在运动的过程中,设△PEF与△ABD重叠部分面积为S,请求出S与t的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“早黑宝”是我省农科院研制的优质新品种,在我省被广泛种植.清徐县某葡萄种植基地2016年种植“早黑宝”100亩,到2018年“早黑宝”的种植面积达到225亩.
(1)求该基地这两年“早黑宝”种植面积的平均增长率;
(2)市场调查发现,当“早黑宝”售价为20元/千克时,每天能售出200千克,售价每降低1元,每天可多售出50千克,为了推广宣传,基地决定降价促销,已知该基地“早黑宝”的平均成本价为12元/千克,若使销售“早黑宝”每天获利1800元,则售价应降低多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
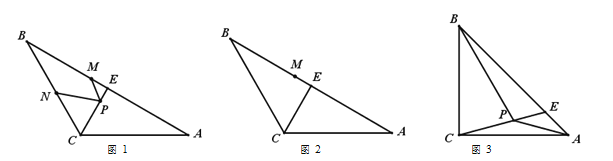
【题目】在△ABC 中,AC=BC,点 E 在是 AB 边上一动点(不与 A、B 重合),连接 CE,点 P 是直线 CE 上一个动点.
(1)如图 1,∠ACB=120°,AB=16,E 是 AB 中点,EM=2,N 是射线 CB 上一个动点, 若使得 NP+MP 的值最小,应如何确定 M 点和点 N 的位置?请你在图 2 中画出点 M 和点 N 的位置,并简述画法: 直接写出 NP+MP 的最小值
(2)如图 3,∠ACB=90°,连接 BP, BPC=75°且 BC=BP.求证:PC=PA.
查看答案和解析>>
科目:初中数学 来源: 题型:
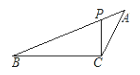
【题目】如图,在△ABC中,点P在AB上,下列四个条件中:①∠ACP=∠B;②∠APC=∠ACB;③AC2=APAB;④ABCP=APCB,能满足△APC与△ACB相似的条件有______________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com