
【题目】如图1, △ABC中,CD⊥AB于D,且BD: AD:CD=2:3:4,
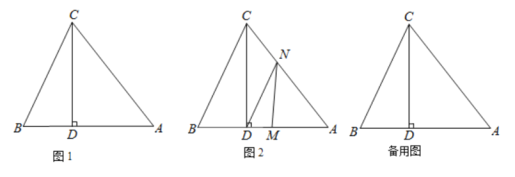
(1)试说明△ABC是等腰三角形;
(2)已知S△ABC=40cm2,如图2,动点M从点B出发以每秒1cm的速度沿线段BA向点A运动,同时动点N从点A出发以相同速度沿线段AC向点C运动,当其中一点到达终点时整个运动都停止.设点M运动的时间为t(秒),若△DMN的边与BC平行,求t的值;
【答案】(1)见解析(2)5或6.
【解析】
(1)设BD=2x,AD=3x,CD=4x,则AB=5x,由勾股定理求出AC,即可得出结论;
(2)由△ABC的面积求出BD、AD、CD、AC;当MN∥BC时,AM=AN;当DN∥BC时,AD=AN;得出方程,解方程即可.
(1)证明:设BD=2x,AD=3x,CD=4x,
则AB=5x,
在Rt△ACD中,AC=![]() =5x,
=5x,
∴AB=AC,
∴△ABC是等腰三角形;
(2)S△ABC=![]() ×5x×4x=40cm2,而x>0,
×5x×4x=40cm2,而x>0,
∴x=2cm,
则BD=4cm,AD=6cm,CD=8cm,AC=10cm.
①当MN∥BC时,AM=AN,
即10t=t,
∴t=5;
当DN∥BC时,AD=AN,
得:t=6;
∴若△DMN的边与BC平行时,t值为5或6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】班级组织同学乘大巴车前往“研学旅行”基地开展爱国教育活动,基地离学校有90公里,队伍8:00从学校出发.苏老师因有事情,8:30从学校自驾小车以大巴1.5倍的速度追赶,追上大巴后继续前行,结果比队伍提前15分钟到达基地.问:
(1)大巴与小车的平均速度各是多少?
(2)苏老师追上大巴的地点到基地的路程有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列各组条件中,不能说明![]() 的是( )
的是( )
A.AB=DE,∠B=∠E,∠C=∠FB.AB=DE,∠A=∠D,∠B=∠E
C.AC=DF,BC=EF,∠A=∠DD.AB=DE,BC=EF,AC=ED
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小方家住户型呈长方形,平面图如下(单位:米),现准备铺设地面,三间卧室铺设木地板,其它区城铺设地砖.
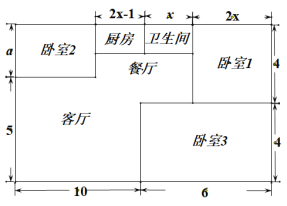
(1)求a的值.
(2)铺设地面需要木地板和地砖各多少平方米(用含![]() 的代数式表示)?
的代数式表示)?
(3)按市场价格,木地板单价为300元/平方米,地砖单价为100元/平方米,装修公司有![]() 两种活动方案,如表:
两种活动方案,如表:
活动方案 | 木地板价格 | 地砖价格 | 总安装费 |
A | 8折 | 8.5折 | 2000元 |
B | 9折 | 8.5折 | 免收 |
已知卧室2的面积是21平方米,则小方家应选择哪种活动,使铺设地面的总费用(包括材料费及安装费)更低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列5个结论:
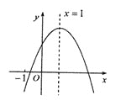
①abc>0;②b>a+c;③9a+3b+c>0; ④c<-3a; ⑤a+b≥m(am+b),其中正确的有( )
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
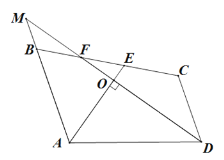
【题目】如图,四边形 ABCD 中,AE,DF 分别是∠BAD,∠ADC 的平分线,且 AE⊥DF 于点 O . 延长 DF 交 AB 的延长线于点 M .
(1)求证:AB∥DC ;
(2)若∠MBC=120°,∠BAD=108°,求∠C,∠DFE 的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是按照一定规律画出的一列“树型”图:
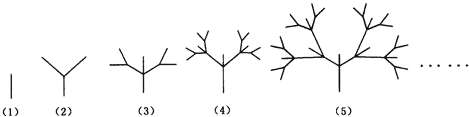
经观察可以发现:图(2)比图(1)多出2个“树枝”,图(3)比图(2)多出5个“树枝”,图(4)比图(3)多出10个“树枝”,照此规律,图(7)比图(6)多出_____个“树枝”.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)问题发现:如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE,则∠AEB的度数为 ,线段AD、BE之间的关系 .
(2)拓展探究:如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.①请判断∠AEB的度数,并说明理由;②当CM=5时,AC比BE的长度多6时,求AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.
(1)如图1,点E,F在AB,AC上,且∠EDF=90°.求证:BE=AF;
(2)点M,N分别在直线AD,AC上,且∠BMN=90°.
①如图2,当点M在AD的延长线上时,求证:AB+AN=![]() AM;
AM;
②当点M在点A,D之间,且∠AMN=30°时,已知AB=2,直接写出线段AM的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com