
”¾ĢāÄæ”æ³Ģ“óĪ»ŹĒĪŅ¹śĆ÷³ÆÉĢČĖ£¬ÖéĖć·¢Ć÷¼Ņ![]() Ėū60ĖźŹ±Ķź³ÉµÄ
Ėū60ĖźŹ±Ķź³ÉµÄ![]() Ö±ÖøĖć·ØĶ³×Ś
Ö±ÖøĖć·ØĶ³×Ś![]() ŹĒ¶«·½¹Å“śŹżŃ§ĆūÖų£¬ĻźŹöĮĖ“«Ķ³µÄÖéĖć¹ęŌņ£¬Č·Į¢ĮĖĖćÅĢÓĆ·Ø
ŹĒ¶«·½¹Å“śŹżŃ§ĆūÖų£¬ĻźŹöĮĖ“«Ķ³µÄÖéĖć¹ęŌņ£¬Č·Į¢ĮĖĖćÅĢÓĆ·Ø![]() ¶ŌŹé֊ijŅ»ĪŹĢāøıąČēĻĀ£ŗ
¶ŌŹé֊ijŅ»ĪŹĢāøıąČēĻĀ£ŗ
Ņ»°ŁĀųĶ·Ņ»°ŁÉ®£¬“óɮȿøöøüĪŽÕł£»
Š”ɮȿČĖ·ÖŅ»øö£¬“óÉ®¹²µĆ¼øĀųĶ·£®
Ņ»°ŁĀųĶ·Ņ»°ŁÉ®£¬“óɮȿøöøüĪŽÕł£»
Š”ɮȿČĖ·ÖŅ»øö£¬“óÉ®¹²µĆ¼øĀųĶ·£®
ŅāĖ¼ŹĒ£ŗÓŠ100øöŗĶÉŠ·Ö100øöĀųĶ·£¬Čē¹ū“óŗĶÉŠ1ČĖ·Ö3øö£¬Š”ŗĶÉŠ3ČĖ·Ö1øöÕżŗĆ·ÖĶź£¬“óŗĶÉŠ¹²·ÖµĆ![]() ””””
””””![]() øöĀųĶ·
øöĀųĶ·
A. 25B. 72C. 75D. 90

| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŌŚĘ½ĆęÖ±½Ē×ų±źĻµÖŠ£¬ĪŅĆĒ¶ØŅåÖ±Ļßy=ax-aĪŖÅ×ĪļĻßy=ax2+bx+c£Øa”¢b”¢cĪŖ³£Źż£¬a”Ł0£©µÄ”°ŃÜÉśÖ±Ļß”±£»ÓŠŅ»øö¶„µćŌŚÅ×ĪļĻßÉĻ£¬ĮķÓŠŅ»øö¶„µćŌŚyÖįÉĻµÄČż½ĒŠĪĪŖĘä”°ŃÜɜȿ½ĒŠĪ”±£®ŅŃÖŖÅ×ĪļĻß![]() ÓėĘä”°ŃÜÉśÖ±Ļß”±½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ×ó²ą£©£¬ÓėxÖįøŗ°ėÖį½»ÓŚµćC£®
ÓėĘä”°ŃÜÉśÖ±Ļß”±½»ÓŚA”¢BĮ½µć£ØµćAŌŚµćBµÄ×ó²ą£©£¬ÓėxÖįøŗ°ėÖį½»ÓŚµćC£®

£Ø1£©ĢīæÕ£ŗøĆÅ×ĪļĻߵĔ°ŃÜÉśÖ±Ļß”±µÄ½āĪöŹ½ĪŖ £¬µćAµÄ×ų±źĪŖ £¬µćBµÄ×ų±źĪŖ £»
£Ø2£©ČēĶ¼£¬µćMĪŖĻ߶ĪCBÉĻŅ»¶Æµć£¬½«”÷ACMŅŌAMĖłŌŚÖ±ĻßĪŖ¶Ō³ĘÖį·ÕŪ£¬µćCµÄ¶Ō³ĘµćĪŖN£¬Čō”÷AMNĪŖøĆÅ×ĪļĻߵĔ°ŃÜɜȿ½ĒŠĪ”±£¬ĒóµćNµÄ×ų±ź£»
£Ø3£©µ±µćEŌŚÅ×ĪļĻߵĶŌ³ĘÖįÉĻŌĖ¶ÆŹ±£¬ŌŚøĆÅ×ĪļĻߵĔ°ŃÜÉśÖ±Ļß”±ÉĻ£¬ŹĒ·ń“ęŌŚµćF£¬Ź¹µĆŅŌµćA”¢C”¢E”¢FĪŖ¶„µćµÄĖıߊĪĪŖĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬ĒėÖ±½ÓŠ“³öµćE”¢FµÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻß![]() ¾¹ż
¾¹ż![]() Čżµć
Čżµć
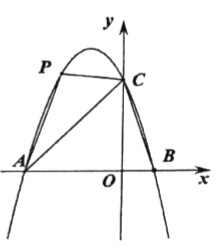
£Ø1£©ĒóÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©ŌŚÖ±Ļß![]() ÉĻ·½µÄÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚŅ»µć
ÉĻ·½µÄÅ×ĪļĻßÉĻŹĒ·ń“ęŌŚŅ»µć![]() £¬Ź¹
£¬Ź¹![]() µÄĆ껿µČÓŚ
µÄĆ껿µČÓŚ![]() µÄĆ껿µÄŅ»°ė£æČō“ęŌŚ£¬Ēó³öµć
µÄĆ껿µÄŅ»°ė£æČō“ęŌŚ£¬Ēó³öµć![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£»
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĖµĆ÷ĄķÓÉ£»
£Ø3£©µć![]() ĪŖÅ×ĪļĻßÉĻŅ»¶Æµć£¬ŌŚ
ĪŖÅ×ĪļĻßÉĻŅ»¶Æµć£¬ŌŚ![]() ÖįÉĻŹĒ·ń“ęŌŚµć
ÖįÉĻŹĒ·ń“ęŌŚµć![]() £¬Ź¹ŅŌ
£¬Ź¹ŅŌ![]() £¬
£¬![]() £¬
£¬![]() £¬
£¬![]() ĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬Ēó³öµć
ĪŖ¶„µćµÄĖıߊĪŹĒĘ½ŠŠĖıߊĪ£æČō“ęŌŚ£¬Ēó³öµć![]() µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
µÄ×ų±ź£»Čō²»“ęŌŚ£¬ĒėĖµĆ÷ĄķÓÉ£®
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æŅŃÖŖ£ŗČēĶ¼£¬ŌŚ![]() ÖŠ£¬
ÖŠ£¬![]() £¬
£¬![]() £¬“¹×ćĪŖµć
£¬“¹×ćĪŖµć![]() £¬
£¬![]() ŹĒ
ŹĒ![]() Ķā½Ē
Ķā½Ē![]() µÄĘ½·ÖĻߣ¬
µÄĘ½·ÖĻߣ¬![]() £¬“¹×ćĪŖµć
£¬“¹×ćĪŖµć![]() £¬Į¬½Ó
£¬Į¬½Ó![]() ½»
½»![]() ÓŚµć
ÓŚµć![]() £®
£®
![]() ĒóÖ¤£ŗĖıߊĪ
ĒóÖ¤£ŗĖıߊĪ![]() ĪŖ¾ŲŠĪ£»
ĪŖ¾ŲŠĪ£»
![]() µ±
µ±![]() Āś×ćŹ²Ć“Ģõ¼žŹ±£¬ĖıߊĪ
Āś×ćŹ²Ć“Ģõ¼žŹ±£¬ĖıߊĪ![]() ŹĒŅ»øöÕż·½ŠĪ£æ²¢øų³öÖ¤Ć÷£®
ŹĒŅ»øöÕż·½ŠĪ£æ²¢øų³öÖ¤Ć÷£®
![]() ŌŚ
ŌŚ![]() µÄĢõ¼žĻĀ£¬Čō
µÄĢõ¼žĻĀ£¬Čō![]() £¬ĒóÕż·½ŠĪ
£¬ĒóÕż·½ŠĪ![]() Öܳ¤£®
Öܳ¤£®

²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŅŃÖŖÅ×ĪļĻßy£½©x2+bx+3µÄ¶Ō³ĘÖįĪŖÖ±Ļßx£½©1£¬·Ö±šÓėxÖį½»ÓŚµćA£¬B£ØAŌŚBµÄ×ó²ą£©£¬ÓėyÖį½»ÓŚµćC£®
£Ø1£©ĒóbµÄÖµ£»
£Ø2£©Čō½«Ļ߶ĪBCČʵćCĖ³Ź±ÕėŠż×Ŗ90”ćµĆµ½Ļ߶ĪCD£¬ĪŹ£ŗµćDŌŚøĆÅ×ĪļĻßÉĻĀš£æĒėĖµĆ÷ĄķÓÉ£®
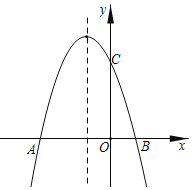
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬ŌŚ![]() ÖŠ£¬µć
ÖŠ£¬µć![]() ŌŚŠ±±ß
ŌŚŠ±±ß![]() ÉĻ£¬ŅŌ
ÉĻ£¬ŅŌ![]() ĪŖŌ²ŠÄ£¬
ĪŖŌ²ŠÄ£¬![]() ĪŖ°ė¾¶×÷Ō²£¬·Ö±šÓė
ĪŖ°ė¾¶×÷Ō²£¬·Ö±šÓė![]() ”¢
”¢![]() Ļą½»ÓŚµć
Ļą½»ÓŚµć![]() ”¢
”¢![]() £¬Į¬½Ó
£¬Į¬½Ó![]() £¬ŅŃÖŖ
£¬ŅŃÖŖ![]() .
.
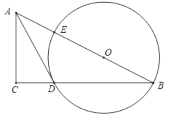
£Ø1£©ĒóÖ¤£ŗ![]() ŹĒ
ŹĒ![]() µÄĒŠĻߣ»
µÄĒŠĻߣ»
£Ø2£©Čō![]() £¬
£¬![]() £¬ĒóĮÓ»”
£¬ĒóĮÓ»”![]() ÓėĻŅ
ÓėĻŅ![]() ĖłĪ§ŅõÓ°Ķ¼ŠĪµÄĆ껿£»
ĖłĪ§ŅõÓ°Ķ¼ŠĪµÄĆ껿£»
£Ø3£©Čō![]() £¬
£¬![]() £¬Ēó
£¬Ēó![]() µÄ³¤.
µÄ³¤.
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ņ»“ĪŗÆŹż![]() Óė·“±ČĄżŗÆŹż
Óė·“±ČĄżŗÆŹż![]() µÄĶ¼Ļó½»ÓŚ
µÄĶ¼Ļó½»ÓŚ![]() Į½µć£¬¹żµć
Į½µć£¬¹żµć![]() ×÷
×÷![]() Öį£¬“¹×ćĪŖµć
Öį£¬“¹×ćĪŖµć![]() £¬ĒŅ
£¬ĒŅ![]() ”£
ӣ
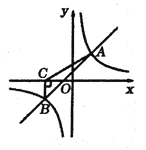
£Ø1£©ĒóŅ»“ĪŗÆŹżÓė·“±ČĄżŗÆŹżµÄ±ķ“ļŹ½£»
£Ø2£©øł¾ŻĖłøųĢõ¼ž£¬ĒėÖ±½ÓŠ“³ö²»µČŹ½![]() µÄ½ā¼Æ£»
µÄ½ā¼Æ£»
£Ø3£©Čō![]() ŹĒ·“±ČĄżŗÆŹż
ŹĒ·“±ČĄżŗÆŹż![]() Ķ¼ĻóÉĻµÄĮ½µć£¬ĒŅ
Ķ¼ĻóÉĻµÄĮ½µć£¬ĒŅ![]() £¬Ē󏵏ż
£¬Ē󏵏ż![]() µÄȔֵ·¶Ī§”£
µÄȔֵ·¶Ī§”£
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Ä³¾ÓĆńĀ„![]() µÄĒ°ĆęÓŠŅ»Ī§Ē½
µÄĒ°ĆęÓŠŅ»Ī§Ē½![]() £¬ŌŚµć
£¬ŌŚµć![]() “¦²āµĆĀ„¶„
“¦²āµĆĀ„¶„![]() µÄŃö½ĒĪŖ
µÄŃö½ĒĪŖ![]() £¬ŌŚ
£¬ŌŚ![]() “¦²āµĆĀ„¶„
“¦²āµĆĀ„¶„![]() µÄŃö½ĒĪŖ
µÄŃö½ĒĪŖ![]() £¬ĒŅ
£¬ĒŅ![]() µÄø߶ČĪŖ2Ć×£¬
µÄø߶ČĪŖ2Ć×£¬![]() Ö®¼äµÄ¾ąĄėĪŖ20Ć×£Ø
Ö®¼äµÄ¾ąĄėĪŖ20Ć×£Ø![]() £¬
£¬![]() £¬
£¬![]() ŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£©.
ŌŚĶ¬Ņ»ĢõÖ±ĻßÉĻ£©.
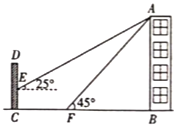
£Ø1£©Ēó¾ÓĆńĀ„![]() µÄø߶Č.
µÄø߶Č.
£Ø2£©ĒėÄćĒó³ö![]() ”¢
”¢![]() Į½µćÖ®¼äµÄ¾ąĄė.£Ø²Īæ¼Źż¾Ż£ŗ
Į½µćÖ®¼äµÄ¾ąĄė.£Ø²Īæ¼Źż¾Ż£ŗ![]() £¬
£¬![]() £¬
£¬![]() £¬½į¹ū±£ĮōÕūŹż£©
£¬½į¹ū±£ĮōÕūŹż£©
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ
”¾ĢāÄæ”æČēĶ¼£¬Å×ĪļĻßy£½ax2©![]() x+cÓėxÖįĻą½»ÓŚµćA£Ø©2£¬0£©”¢B£Ø4£¬0£©£¬ÓėyÖįĻą½»ÓŚµćC£¬Į¬½ÓAC£¬BC£¬ŅŌĻ߶ĪBCĪŖÖ±¾¶×÷”ŃM£¬¹żµćC×÷Ö±ĻßCE”ĪAB£¬ÓėÅ×ĪļĻßŗĶ”ŃM·Ö±š½»ÓŚµćD£¬E£¬µćPŌŚBCĻĀ·½µÄÅ×ĪļĻßÉĻŌĖ¶Æ£®
x+cÓėxÖįĻą½»ÓŚµćA£Ø©2£¬0£©”¢B£Ø4£¬0£©£¬ÓėyÖįĻą½»ÓŚµćC£¬Į¬½ÓAC£¬BC£¬ŅŌĻ߶ĪBCĪŖÖ±¾¶×÷”ŃM£¬¹żµćC×÷Ö±ĻßCE”ĪAB£¬ÓėÅ×ĪļĻßŗĶ”ŃM·Ö±š½»ÓŚµćD£¬E£¬µćPŌŚBCĻĀ·½µÄÅ×ĪļĻßÉĻŌĖ¶Æ£®
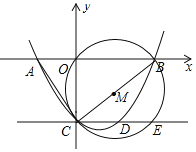
£Ø1£©ĒóøĆÅ×ĪļĻߵĽāĪöŹ½£»
£Ø2£©µ±”÷PDEŹĒŅŌDEĪŖµ×±ßµÄµČŃüČż½ĒŠĪŹ±£¬ĒóµćPµÄ×ų±ź£»
£Ø3£©µ±ĖıߊĪACPBµÄĆ껿×ī“óŹ±£¬ĒóµćPµÄ×ų±ź²¢Ēó³ö×ī“óÖµ£®
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com