
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C;延长C1B1交x轴于点A2,作正方形A2B2C2C1…按这样的规律进行下去,第1个正方形的面积为___;第4个正方形的面积为___.

【答案】5 ![]()
【解析】
由点A的坐标为(1,0),点D的坐标为(0,2).即可求得OA与OD的长,然后由勾股定理即可求得AD的长,继而求得第1个正方形ABCD的面积;先证得△DOA∽△ABA1,然后由相似三角形的对应边成比例,可求得A1B的长,即可求得A1C的长,即可得第2个正方形A1B1C1C的面积;以此类推,可得第3个、第4个正方形的面积.
∵点A的坐标为(1,0),点D的坐标为(0,2).
∴OA=1,OD=2,
在Rt△AOD中,AD=![]() =
=![]() ,
,
∴正方形ABCD的面积为:![]() ;
;
∵四边形ABCD是正方形,
∴AD=AB,∠DAB=∠ABC=∠ABA1=90°=∠DOA,
∴∠ADO+∠DAO=90°,∠DAO+∠BA A1=90°,
∴∠ADO=∠BA A1,
∵∠DOA=∠AB A1,
∴△DOA∽△AB A1,
∴![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:A1B=![]() ,
,
∴A1C= A1B+BC=![]() ,
,
∴正方形A1B1C1C的面积为: 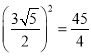 ;
;
∵第1个正方形ABCD的面积为:5;
第2个正方形A1 B1 C1C的面积为:![]() =
=![]() ×5;
×5;
同理可得:第3个正方形A2 B2 C2 C1的面积为:![]() ×
×![]() ×5=
×5=![]() ;
;
∴第4个正方形A3 B3 C3C2的面积为:![]() .
.
故答案为:5, ![]()


科目:初中数学 来源: 题型:
【题目】甲、乙两支仪仗队队员的身高(单位:厘米)如下:
甲队:178,177,179,178,177,178,177,179,178,179;
乙队:178,179,176,178,180,178,176,178,177,180;
(1)甲队队员身高的平均数为 厘米,乙队队员身高的平均数为 厘米;
(2)你认为哪支仪仗队更为整齐?简要说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( ).
A. “打开电视机,正在播放《动物世界》”是必然事件
B. 某种彩票的中奖概率为![]() ,说明每买1000张,一定有一张中奖
,说明每买1000张,一定有一张中奖
C. 抛掷一枚质地均匀的硬币一次,出现正面朝上的概率为![]()
D. 想了解长沙市所有城镇居民的人均年收入水平,宜采用抽样调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是△ACD的外接圆⊙O的直径,CD交AB于点F,其中AC=AD,AD的延长线交过点B的切线BM于点E.
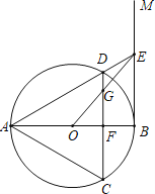
(1)求证:CD∥BM;
(2)连接OE交CD于点G,若DE=2,AB=4![]() ,求OG的长.
,求OG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
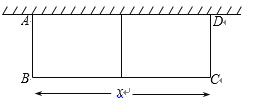
【题目】如图,利用一面墙(墙的长度为15 m),用篱笆围成一个矩形花园ABCD,中间再用一道篱笆隔成两个小矩形,共用去篱笆42 m.设平行于墙的一边BC长为x m,花园的面积为S m2.
(1)求S与x之间的函数解析式;
(2)问花园面积可以达到120平方米吗?如果能,花园的长和宽各是多少?如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,AC,BC是⊙O的两条弦,过点C作∠BCD=∠A,CD交AB的延长线与点D.
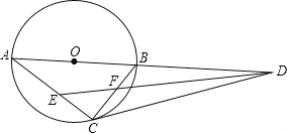
(1)求证:CD是⊙O的切线;
(2)若tanA=![]() ,求
,求![]() 的值;
的值;
(3)在(2)的条件下,若AB=7,∠CED=∠A+∠EDC,求EC与ED的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
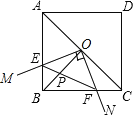
【题目】如图,已知在正方形ABCD中,点O是对角线AC的中点,过O点的射线OM、ON分别交AB、BC于点E、F,且∠EOF=90°,BO、EF交于点P,下列结论:
①图形中全等的三角形只有三对; ②△EOF是等腰直角三角形;③正方形ABCD的面积等于四边形OEBF面积的4倍;④BE+BF=OA;⑤AE2+BE2=2OPOB.其中正确的个数有( )个.
A. 4B. 3C. 2D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
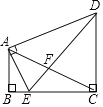
【题目】如图,四边形ABCD中,∠ABC=∠BCD=90°,AB=1,AE⊥AD,交BC于点E,EA平分∠BED.
(1)CD的长是_____;
(2)当点F是AC中点时,四边形ABCD的周长是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com