
【题目】教材呈现:如图是华师版九年级上册数学教材第78页的部分内容.
例2 如图,在![]() 中,
中,![]() 分别是边
分别是边![]() 的中点,
的中点,![]() 相交于点
相交于点![]() ,求证:
,求证:![]() ,
,
证明:连结![]() .
.
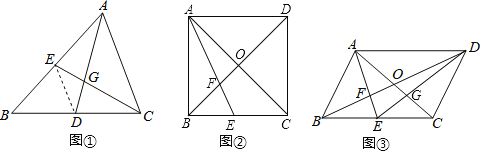
请根据教材提示,结合图①,写出完整的证明过程.
结论应用:在![]() 中,对角线
中,对角线![]() 交于点
交于点![]() ,
,![]() 为边
为边![]() 的中点,
的中点,![]() 、
、![]() 交于点
交于点![]() .
.
(1)如图②,若![]() 为正方形,且
为正方形,且![]() ,则
,则![]() 的长为 .
的长为 .
(2)如图③,连结![]() 交
交![]() 于点
于点![]() ,若四边形
,若四边形![]() 的面积为
的面积为![]() ,则
,则![]() 的面积为 .
的面积为 .
![]()
【答案】教材呈现:详见解析;结论应用:(1)![]() ;(2)6.
;(2)6.
【解析】
教材呈现:如图①,连结![]() .根据三角形中位线定理可得
.根据三角形中位线定理可得![]() ,
,![]() ,那么
,那么![]() ,由相似三角形对应边成比例以及比例的性质即可证明
,由相似三角形对应边成比例以及比例的性质即可证明![]() ;
;
结论应用:(1)如图②.先证明![]() ,得出
,得出![]() ,那么
,那么![]() ,又
,又![]() ,可得
,可得![]() ,由正方形的性质求出
,由正方形的性质求出![]() ,即可求出
,即可求出![]() ;
;
(2)如图③,连接![]() .由(1)易证
.由(1)易证![]() .根据同高的两个三角形面积之比等于底边之比得出
.根据同高的两个三角形面积之比等于底边之比得出![]() 与
与![]() 的面积比
的面积比![]() ,同理,
,同理,![]() 与
与![]() 的面积比=2,那么
的面积比=2,那么![]() 的面积
的面积![]() 的面积=2(
的面积=2(![]() 的面积
的面积![]() 的面积)=
的面积)=![]() ,所以
,所以![]() 的面积
的面积![]() ,进而求出
,进而求出![]() 的面积
的面积![]() .
.
教材呈现:
证明:
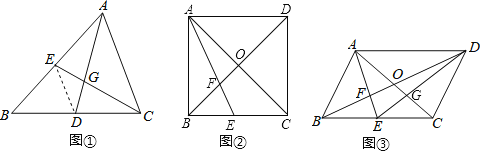
如图①,连结![]() .
.
∵在![]() 中,
中,![]() 分别是边
分别是边![]() 的中点,
的中点,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ;
;
结论应用:
(1)解:如图②.
∵四边形![]() 为正方形,
为正方形,![]() 为边
为边![]() 的中点,对角线
的中点,对角线![]() 、
、![]() 交于点
交于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵正方形![]() 中,
中,![]() ,
,
∴![]() ,
,
∴![]() .
.
故答案为![]() ;
;
(2)解:如图③,连接![]() .
.
由(1)知,![]() ,
,
∴![]() .
.
∵![]() 与
与![]() 的高相同,
的高相同,
∴![]() 与
与![]() 的面积比
的面积比![]() ,
,
同理,![]() 与
与![]() 的面积比=2,
的面积比=2,
∴![]() 的面积
的面积![]() 的面积=2(
的面积=2(![]() 的面积
的面积![]() 的面积)
的面积)![]() ,
,
∴![]() 的面积
的面积![]() ,
,
∴![]() 的面积
的面积![]() .
.
故答案为6.


科目:初中数学 来源: 题型:
【题目】如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )

A. PA=PBB. ∠BPD=∠APDC. AB⊥PDD. AB平分PD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月12日是第41个植树节,某单位积极开展植树活动,决定购买甲、乙两种树苗,用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗每棵比甲种树苗每棵少6元.
(1)求甲种树苗每棵多少元?
(2)若准备用3800元购买甲、乙两种树苗共100棵,则至少要购买乙种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
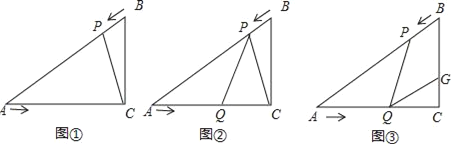
【题目】已知:如图,在Rt△ACB中,∠C=90°,BC=3cm,AC=3![]() cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为
cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为![]() cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题:
cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题:
(1)如图①,连接PC,当t为何值时△APC∽△ACB,并说明理由;
(2)如图②,当点P,Q运动时,是否存在某一时刻t,使得点P在线段QC的垂直平分线上,请说明理由;
(3)如图③,当点P,Q运动时,线段BC上是否存在一点G,使得四边形PQGB为菱形?若存在,试求出BG长;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC内接于半圆,AB为直径,过点A作直线MN,若∠MAC=∠ABC.

(1)求证:MN是半圆的切线.
(2)设D是弧AC的中点,连接BD交AC于G,过D作DE⊥AB于E,交AC于F,求证:FD=FG.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队需完成A、B两个工地的工程.若甲、乙两个工程队分别可提供40个和50个标准工作量,完成A、B两个工地的工程分别需要70个和20个标准工作量,且两个工程队在A、B两个工地的1个标准工作量的成本如下表所示:
A工地 | B工地 | |
甲工程队 | 800元 | 750元 |
乙工程队 | 600元 | 570元 |
设甲工程队在A工地投入x(20≤x≤40)个标准工作量,完成这两个工程共需成本y元.
(1)求y与x之间的函数关系式;
(2)请判断y是否能等于62000,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
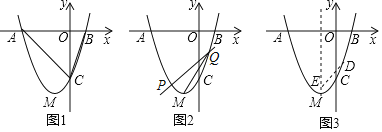
【题目】如图1,抛物线y=ax2+2ax+c与x轴交于A(-3,0)、B两点,与y轴交于C点,△ABC的面积为6,抛物线顶点为M.
(1)如图1,求抛物线的解析式;
(2)如图2,直线y=kx+k-3与抛物线交于P、Q两点(P点在Q点左侧),问在y轴上是否存在点N,使四边形PMQN为矩形?若存在,求N点坐标,若不存在,请说明理由;
(3)如图3,若D为抛物线上任意一点,E(-1,s)为对称轴上一点,若对任意一点D都有ED≥EM,求s的最大值及相应E点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两条抛物线![]() 与
与![]() 的顶点相同.
的顶点相同.
(1)求抛物线![]() 的解析式;
的解析式;
(2)点![]() 是抛物找
是抛物找![]() 在第四象限内图象上的一动点,过点
在第四象限内图象上的一动点,过点![]() 作
作![]() 轴,
轴,![]() 为垂足,求
为垂足,求![]() 的最大值;
的最大值;
(3)设抛物线![]() 的顶点为点
的顶点为点![]() ,点
,点![]() 的坐标为
的坐标为![]() ,问在
,问在![]() 的对称轴上是否存在点
的对称轴上是否存在点![]() ,使线段
,使线段![]() 绕点
绕点![]() 顺时针旋转90°得到线段
顺时针旋转90°得到线段![]() ,且点
,且点![]() 恰好落在抛物线
恰好落在抛物线![]() 上?若存在,求出点
上?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com