
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌдкRtЁїACBжаЃЌЁЯC=90ЁуЃЌBC=3cmЃЌAC=3![]() cmЃЌЕуPгЩBЕуГіЗЂбиBAЗНЯђЯђЕуAдШЫйдЫЖЏЃЌЫйЖШЮЊ2cm/sЃЛЕуQгЩAЕуГіЗЂбиACЗНЯђЯђЕуCдШЫйдЫЖЏЃЌЫйЖШЮЊ
cmЃЌЕуPгЩBЕуГіЗЂбиBAЗНЯђЯђЕуAдШЫйдЫЖЏЃЌЫйЖШЮЊ2cm/sЃЛЕуQгЩAЕуГіЗЂбиACЗНЯђЯђЕуCдШЫйдЫЖЏЃЌЫйЖШЮЊ![]() cm/sЃЛШєЩшдЫЖЏЕФЪБМфЮЊt(s)(0ЃМtЃМ3)ЃЌНтД№ЯТСаЮЪЬтЃК
cm/sЃЛШєЩшдЫЖЏЕФЪБМфЮЊt(s)(0ЃМtЃМ3)ЃЌНтД№ЯТСаЮЪЬтЃК
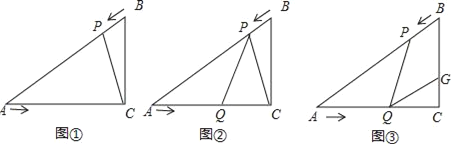
(1)ШчЭМЂйЃЌСЌНгPCЃЌЕБtЮЊКЮжЕЪБЁїAPCЁзЁїACBЃЌВЂЫЕУїРэгЩЃЛ
(2)ШчЭМЂкЃЌЕБЕуPЃЌQдЫЖЏЪБЃЌЪЧЗёДцдкФГвЛЪБПЬtЃЌЪЙЕУЕуPдкЯпЖЮQCЕФДЙжБЦНЗжЯпЩЯЃЌЧыЫЕУїРэгЩЃЛ
(3)ШчЭМЂлЃЌЕБЕуPЃЌQдЫЖЏЪБЃЌЯпЖЮBCЩЯЪЧЗёДцдквЛЕуGЃЌЪЙЕУЫФБпаЮPQGBЮЊСтаЮЃПШєДцдкЃЌЪдЧѓГіBGГЄЃЛШєВЛДцдкЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁП(1)t=![]() ЃЌРэгЩМћНтЮіЃЛ(2)ДцдкЃЌt=1ЃЌРэгЩМћНтЮіЃЛ(3)ВЛДцдкЃЌРэгЩМћНтЮі.
ЃЌРэгЩМћНтЮіЃЛ(2)ДцдкЃЌt=1ЃЌРэгЩМћНтЮіЃЛ(3)ВЛДцдкЃЌРэгЩМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉНсКЯжБНЧШ§НЧаЮаджЪЃЌгЩЁїAPCЁзЁїACBЃЌЕУ![]() ЃЛЃЈ2ЃЉЙ§ЕуPзїPMЁЭACЃЌИљОнЯпЖЮДЙжБЦНЗжЯпаджЪЃЌЧѓQM,AMЕФБэДяЪНЃЌжЄЁїAPMЁзЁїABCЃЌЕУ
ЃЛЃЈ2ЃЉЙ§ЕуPзїPMЁЭACЃЌИљОнЯпЖЮДЙжБЦНЗжЯпаджЪЃЌЧѓQM,AMЕФБэДяЪНЃЌжЄЁїAPMЁзЁїABCЃЌЕУ ![]() ЃЌ
ЃЌ ЃЛЃЈ3ЃЉМйЩшЯпЖЮBCЩЯЪЧДцдквЛЕуGЃЌЪЙЕУЫФБпаЮPQGBЮЊЦНааЫФБпаЮЃЌдђPQЁЮBGЃЌPQ=BGЃЌгЩЁїAPQЁзЁїABCЃЌЕУ
ЃЛЃЈ3ЃЉМйЩшЯпЖЮBCЩЯЪЧДцдквЛЕуGЃЌЪЙЕУЫФБпаЮPQGBЮЊЦНааЫФБпаЮЃЌдђPQЁЮBGЃЌPQ=BGЃЌгЩЁїAPQЁзЁїABCЃЌЕУ![]() ЃЌ
ЃЌ![]() ЕУBP=2t=3ЃЌЙЪPQЁйBP.
ЕУBP=2t=3ЃЌЙЪPQЁйBP.
(1)дкRtЁїACBжаЃЌЁЯC=90ЁуЃЌAC=3![]() cmЃЌBC=3cmЃЌ
cmЃЌBC=3cmЃЌ
ЁрAB=6ЃЌ
гЩдЫЖЏжЊЃЌBP=2tЃЌAQ= ![]() ЃЌ
ЃЌ
ЁрAP=6Љ2tЃЌ
ЁпЁїAPCЁзЁїACBЃЌ
![]()
Ёрt= ![]() ЃЛ
ЃЛ
(2)ДцдкЃЌ
РэгЩЃКШчЭМЂкЃЌгЩдЫЖЏжЊЃЌBP=2tЃЌAQ=![]() ЃЌ
ЃЌ
ЁрAP=6Љ2tЃЌCQ= ![]() ЃЌ
ЃЌ
ЁпЕуPЪЧCQЕФДЙжБЦНЗжЯпЩЯЃЌ
Й§ЕуPзїPMЁЭACЃЌ
ЁрQM=CM= ![]()

ЁрAM=AQ+QM= ![]() =
=![]() (3+t)
(3+t)
ЁпЁЯACB=90ЁуЃЌЁрPMЁЮBCЃЌ
ЁрЁїAPMЁзЁїABC
Ёр ![]()

ЁрНтЕУt=1ЃЛ
(3)ВЛДцдк
РэгЩЃКгЩдЫЖЏжЊЃЌBP=2tЃЌ![]() ЃЌ
ЃЌ
ЁрAP=6Љ2tЃЌ
МйЩшЯпЖЮBCЩЯЪЧДцдквЛЕуGЃЌЪЙЕУЫФБпаЮPQGBЮЊЦНааЫФБпаЮЃЌ
ЁрPQЁЮBGЃЌPQ=BGЃЌ
ЁрЁїAPQЁзЁїABCЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрBP=2t=3ЃЌ
ЁрPQЁйBPЃЌ
ЁрЦНааЫФБпаЮPQGBВЛПЩФмЪЧСтаЮЃЎМДЃКЯпЖЮBCЩЯВЛДцдквЛЕуGЃЌЪЙЕУЫФБпаЮPQGBЮЊСтаЮЃЎ


 ГіВЪЭЌВНДѓЪдОэЯЕСаД№АИ
ГіВЪЭЌВНДѓЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊХзЮяЯп![]() КЭжБЯпl:y=kx+bЃЌЕуA(-3,-3)ЃЌB(1,-1)ОљдкжБЯпlЩЯЃЎ
КЭжБЯпl:y=kx+bЃЌЕуA(-3,-3)ЃЌB(1,-1)ОљдкжБЯпlЩЯЃЎ
ЃЈ1ЃЉШєХзЮяЯпCгыжБЯпlгаНЛЕуЃЌЧѓaЕФШЁжЕЗЖЮЇЃЛ
ЃЈ2ЃЉЕБa=-1ЃЌЖўДЮКЏЪ§![]() ЕФздБфСПxТњзуmЁмxЁмm+2ЪБЃЌКЏЪ§yЕФзюДѓжЕЮЊ-4ЃЌЧѓmЕФжЕЃЛ
ЕФздБфСПxТњзуmЁмxЁмm+2ЪБЃЌКЏЪ§yЕФзюДѓжЕЮЊ-4ЃЌЧѓmЕФжЕЃЛ
ЃЈ3ЃЉШєХзЮяЯпCгыЯпЖЮABгаСНИіВЛЭЌЕФНЛЕуЃЌЧыжБНгаДГіaЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПеђеўИЎЯыСЫНтЖдЭѕМвДхНјааЁАОЋзМЗіЦЖЁБвЛФъРДДхУёЕФОМУЧщПіЃЌЭГМЦдБаЁРюгУМђЕЅЫцЛњГщбљЕФЗНЗЈЃЌдкШЋДх![]() ЛЇМвЭЅжаЫцЛњГщШЁ
ЛЇМвЭЅжаЫцЛњГщШЁ![]() ЛЇЃЌЕїВщЙ§ШЅвЛФъЕФЪеШыЃЈЕЅЮЛЃКЭђдЊЃЉЃЌДгЖјШЅЙРМЦШЋДхМвЭЅФъЪеШыЧщПіЃЎ
ЛЇЃЌЕїВщЙ§ШЅвЛФъЕФЪеШыЃЈЕЅЮЛЃКЭђдЊЃЉЃЌДгЖјШЅЙРМЦШЋДхМвЭЅФъЪеШыЧщПіЃЎ
вбжЊЕїВщЕУЕНЕФЪ§ОнШчЯТЃК
![]()
![]()
ЮЊСЫБугкМЦЫуЃЌаЁРюдкдЪ§ОнЕФУПИіЪ§ЩЯЖММѕШЅ![]() ЃЌЕУЕНЯТУцЕкЖўзщЪ§ЃК
ЃЌЕУЕНЯТУцЕкЖўзщЪ§ЃК
![]()
![]()
![]() ЧыФугУаЁРюЕУЕНЕФЕкЖўзщЪ§МЦЫует
ЧыФугУаЁРюЕУЕНЕФЕкЖўзщЪ§МЦЫует![]() ЛЇМвЭЅЕФЦНОљФъЪеШыЃЌВЂЙРМЦШЋДхФъЪеШыМАШЋДхМвЭЅФъЪеШЫГЌЙ§
ЛЇМвЭЅЕФЦНОљФъЪеШыЃЌВЂЙРМЦШЋДхФъЪеШыМАШЋДхМвЭЅФъЪеШЫГЌЙ§![]() ЭђдЊЕФАйЗжБШЃЛвбжЊФГМвЭЅЙ§ШЅвЛФъЕФЪеШЫЪЧ
ЭђдЊЕФАйЗжБШЃЛвбжЊФГМвЭЅЙ§ШЅвЛФъЕФЪеШЫЪЧ![]() ЭђдЊЃЌЧыФугУЕїВщЕУЕНЕФЪ§ОнЕФжаЮЛЪ§ЭЦВтИУМвЭЅЕФЪеШыЧщПідкШЋДхДІгкЪВУДЫЎЦНЃП
ЭђдЊЃЌЧыФугУЕїВщЕУЕНЕФЪ§ОнЕФжаЮЛЪ§ЭЦВтИУМвЭЅЕФЪеШыЧщПідкШЋДхДІгкЪВУДЫЎЦНЃП
![]() вбжЊаЁРюЫуЕУЕкЖўзщЪ§ЕФЗНВюЪЧ
вбжЊаЁРюЫуЕУЕкЖўзщЪ§ЕФЗНВюЪЧ![]() ЃЌаЁЭѕвРОнЕкЖўзщЪ§ЕФЗНВюЕУГідЪ§ОнЕФЗНВюЮЊ
ЃЌаЁЭѕвРОнЕкЖўзщЪ§ЕФЗНВюЕУГідЪ§ОнЕФЗНВюЮЊ![]() ЃЌФуШЯЮЊаЁЭѕЕФНсЙће§ШЗТ№ЃПШчЙћВЛе§ШЗЃЌжБНгаДГіФуШЯЮЊе§ШЗЕФНсЙћЃЎ
ЃЌФуШЯЮЊаЁЭѕЕФНсЙће§ШЗТ№ЃПШчЙћВЛе§ШЗЃЌжБНгаДГіФуШЯЮЊе§ШЗЕФНсЙћЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
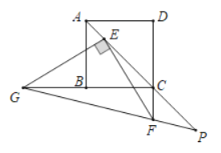
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФЖдНЧЯпACЩЯгавЛЕуEЃЌЧвCEЃН4AEЃЌЕуFдкDCЕФбгГЄЯпЩЯЃЌСЌНгEFЃЌЙ§ЕуEзїEGЁЭEFЃЌНЛCBЕФбгГЄЯпгкЕуGЃЌСЌНгGFВЂбгГЄЃЌНЛACЕФбгГЄЯпгкЕуPЃЌШєABЃН5ЃЌCFЃН2ЃЌдђЯпЖЮEPЕФГЄЪЧ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃКвбжЊЫФБпаЮABCDЪЧЦНааЫФБпаЮЃЌЯТСаНсТлжаВЛе§ШЗЕФЪЧЃЈ ЃЉ
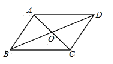
A. ЕБAB=BCЪБЃЌЫќЪЧСтаЮЃЛB. ЕБЁЯABC=90ЁуЪБЃЌЫќЪЧОиаЮЃЛ
C. ЕБAC=BDЪБЃЌЫќЪЧе§ЗНаЮЃЛD. ЕБACЁЭBDЪБЃЌЫќЪЧСтаЮ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌRtЁїABCСНжБНЧБпЕФБпГЄЮЊACЃН3ЃЌBCЃН4ЃЎ
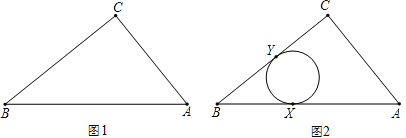
ЃЈ1ЃЉШчЭМ2ЃЌЁбOгыRtЁїABCЕФБпABЯрЧагкЕуXЃЌгыБпBCЯрЧагкЕуYЃЎЧыФудкЭМ2жазїГіВЂБъУїЁбOЕФдВаФЃЈгУГпЙцзїЭМЃЌБЃСєзїЭМКлМЃЃЌВЛаДзїЗЈКЭжЄУїЃЉ
ЃЈ2ЃЉPЪЧетИіRtЁїABCЩЯКЭЦфФкВПЕФЖЏЕуЃЌвдPЮЊдВаФЕФЁбPгыRtЁїABCЕФСНЬѕБпЯрЧаЃЎЩшЁбPЕФУцЛ§ЮЊSЃЌФуШЯЮЊФмЗёШЗЖЈSЕФзюДѓжЕЃПШєФмЃЌЧыФуЧѓГіSЕФзюДѓжЕЃЛШєВЛФмЃЌЧыФуЫЕУїВЛФмШЗЖЈSЕФзюДѓжЕЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
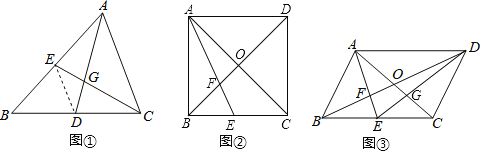
ЁОЬтФПЁПНЬВФГЪЯжЃКШчЭМЪЧЛЊЪІАцОХФъМЖЩЯВсЪ§бЇНЬВФЕк78вГЕФВПЗжФкШнЃЎ
Р§2 ШчЭМЃЌдк![]() жаЃЌ
жаЃЌ![]() ЗжБ№ЪЧБп
ЗжБ№ЪЧБп![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЯрНЛгкЕу
ЯрНЛгкЕу![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЃЌ
ЃЌ
жЄУїЃКСЌНс![]() ЃЎ
ЃЎ
ЧыИљОнНЬВФЬсЪОЃЌНсКЯЭМЂйЃЌаДГіЭъећЕФжЄУїЙ§ГЬЃЎ
НсТлгІгУЃКдк![]() жаЃЌЖдНЧЯп
жаЃЌЖдНЧЯп![]() НЛгкЕу
НЛгкЕу![]() ЃЌ
ЃЌ![]() ЮЊБп
ЮЊБп![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ![]() ЁЂ
ЁЂ![]() НЛгкЕу
НЛгкЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉШчЭМЂкЃЌШє![]() ЮЊе§ЗНаЮЃЌЧв
ЮЊе§ЗНаЮЃЌЧв![]() ЃЌдђ
ЃЌдђ![]() ЕФГЄЮЊЁЁ ЁЁЃЎ
ЕФГЄЮЊЁЁ ЁЁЃЎ
ЃЈ2ЃЉШчЭМЂлЃЌСЌНс![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌШєЫФБпаЮ
ЃЌШєЫФБпаЮ![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЌдђ
ЃЌдђ![]() ЕФУцЛ§ЮЊЁЁ ЁЁЃЎ
ЕФУцЛ§ЮЊЁЁ ЁЁЃЎ
![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
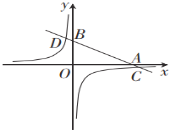
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвЛДЮКЏЪ§![]() ЕФЭМЯѓЗжБ№НЛxжсЁЂyжсгкAЁЂBСНЕуЃЌгыЗДБШР§КЏЪ§
ЕФЭМЯѓЗжБ№НЛxжсЁЂyжсгкAЁЂBСНЕуЃЌгыЗДБШР§КЏЪ§![]() ЕФЭМЯѓНЛгкCЁЂDСНЕу.вбжЊЕуCЕФзјБъЪЧЃЈ6ЃЌ-1ЃЉЃЌDЃЈnЃЌ3ЃЉ.
ЕФЭМЯѓНЛгкCЁЂDСНЕу.вбжЊЕуCЕФзјБъЪЧЃЈ6ЃЌ-1ЃЉЃЌDЃЈnЃЌ3ЃЉ.
ЃЈ1ЃЉЧѓmЕФжЕКЭЕуDЕФзјБъ.
ЃЈ2ЃЉЧѓ![]() ЕФжЕ.
ЕФжЕ.
ЃЈ3ЃЉИљОнЭМЯѓжБНгаДГіЃКЕБxЮЊКЮжЕЪБЃЌвЛДЮКЏЪ§ЕФжЕДѓгкЗДБШР§КЏЪ§ЕФжЕЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЖўДЮКЏЪ§![]() ЕФЭМЯѓЙ§Еу
ЕФЭМЯѓЙ§Еу![]() ЃЌЕу
ЃЌЕу![]() ЃЈ
ЃЈ![]() гы0ВЛжиКЯЃЉЪЧЭМЯѓЩЯЕФвЛЕуЃЌжБЯп
гы0ВЛжиКЯЃЉЪЧЭМЯѓЩЯЕФвЛЕуЃЌжБЯп![]() Й§Еу
Й§Еу![]() ЧвЦНаагк
ЧвЦНаагк![]() жсЃЎ
жсЃЎ![]() гкЕу
гкЕу![]() ЃЌЕу
ЃЌЕу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓжЄЃКЕу![]() дкЯпЖЮ
дкЯпЖЮ![]() ЕФжаДЙЯпЩЯЃЛ
ЕФжаДЙЯпЩЯЃЛ
ЃЈ3ЃЉЩшжБЯп![]() НЛЖўДЮКЏЪ§ЕФЭМЯѓгкСэвЛЕу
НЛЖўДЮКЏЪ§ЕФЭМЯѓгкСэвЛЕу![]() ЃЌ
ЃЌ![]() гкЕу
гкЕу![]() ЃЌЯпЖЮ
ЃЌЯпЖЮ![]() ЕФжаДЙЯпНЛ
ЕФжаДЙЯпНЛ![]() гкЕу
гкЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ4ЃЉЪдХаЖЯЕу![]() гывдЯпЖЮ
гывдЯпЖЮ![]() ЮЊжБОЖЕФдВЕФЮЛжУЙиЯЕЃЎ
ЮЊжБОЖЕФдВЕФЮЛжУЙиЯЕЃЎ
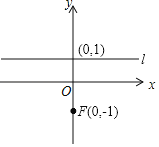
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com