
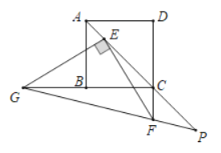
【题目】如图,正方形ABCD的对角线AC上有一点E,且CE=4AE,点F在DC的延长线上,连接EF,过点E作EG⊥EF,交CB的延长线于点G,连接GF并延长,交AC的延长线于点P,若AB=5,CF=2,则线段EP的长是_____.
【答案】![]()
【解析】
如图,作FH⊥PE于H.利用勾股定理求出EF,再证明△CEF∽△FEP,可得EF2=ECEP,由此即可解决问题.
如图,作FH⊥PE于H.
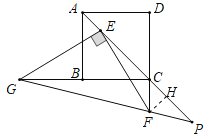
∵四边形ABCD是正方形,AB=5,
∴AC=5![]() ,∠ACD=∠FCH=45°,
,∠ACD=∠FCH=45°,
∵∠FHC=90°,CF=2,
∴CH=HF=![]() ,
,
∵CE=4AE,
∴EC=4![]() ,AE=
,AE=![]() ,
,
∴EH=5![]() ,
,
在Rt△EFH中,EF2=EH2+FH2=(5![]() )2+(
)2+(![]() )2=52,
)2=52,
∵∠GEF=∠GCF=90°,
∴E,G,F,C四点共圆,
∴∠EFG=∠ECG=45°,
∴∠ECF=∠EFP=135°,
∵∠CEF=∠FEP,
∴△CEF∽△FEP,
∴![]() ,
,
∴EF2=ECEP,
∴EP=![]()
故答案为:![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某校为了解九年级学生的体育达标情况,随机抽取![]() 名九年级学生进行体育达标项目测试,测试成绩如下表,请根据表中的信息,解答下列问题:
名九年级学生进行体育达标项目测试,测试成绩如下表,请根据表中的信息,解答下列问题:
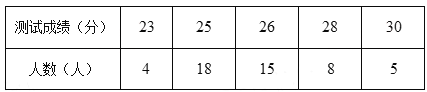
(1)该校九年级有![]() 名学生,估计体育测试成绩为
名学生,估计体育测试成绩为![]() 分的学生人数;
分的学生人数;
(2)该校体育老师要对本次抽测成绩为![]() 分的甲、乙、丙、丁
分的甲、乙、丙、丁![]() 名学生进行分组强化训练,要求两人一组,求甲和乙恰好分在同一组的概率.(用列表或树状图方法解答)
名学生进行分组强化训练,要求两人一组,求甲和乙恰好分在同一组的概率.(用列表或树状图方法解答)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有如图所示的甲、乙、丙、丁四个生产基地.现决定在其中一个基地修建总仓库,以方便公司对各基地生产的产品进行集中存储.已知甲、乙、丙、丁各基地的产量之比等于4:5:4:2,各基地之间的距离之比a:b:c:d:e=2:3:4:3:3(因条件限制,只有图示中的五条运输渠道),当产品的运输数量和运输路程均相等时,所需的运费相等.若要使总运费最低,则修建总仓库的最佳位置为( )
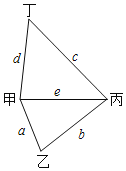
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实,数![]() ,
,![]() ,
,![]() ,用
,用![]() 表示这三个数的平均数,用
表示这三个数的平均数,用![]() 表示这三个数中最小的数,例如
表示这三个数中最小的数,例如![]()
![]() =4,
=4,![]() ,
,![]() .请结合上述材料,解决下列问题:
.请结合上述材料,解决下列问题:
(1)①![]() _____,
_____,
②![]() _____;
_____;
(2)若![]() ,则
,则![]() 的取值范围为_____;
的取值范围为_____;
(3)若![]() ,求
,求![]() 的值;
的值;
(4)如果![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月12日是第41个植树节,某单位积极开展植树活动,决定购买甲、乙两种树苗,用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗每棵比甲种树苗每棵少6元.
(1)求甲种树苗每棵多少元?
(2)若准备用3800元购买甲、乙两种树苗共100棵,则至少要购买乙种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一艘轮船在相距90千米的甲、乙两地之间匀速航行,从甲地到乙地顺流航行用6小时,逆流航行比顺流航行多用4小时.
(1)求该轮船在静水中的速度和水流速度;
(2)若在甲、乙两地之间建立丙码头,使该轮船从甲地到丙地和从乙地到丙地所用的航行时间相同,问甲、丙两地相距多少干米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在Rt△ACB中,∠C=90°,BC=3cm,AC=3![]() cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为
cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为![]() cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题:
cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题:
(1)如图①,连接PC,当t为何值时△APC∽△ACB,并说明理由;
(2)如图②,当点P,Q运动时,是否存在某一时刻t,使得点P在线段QC的垂直平分线上,请说明理由;
(3)如图③,当点P,Q运动时,线段BC上是否存在一点G,使得四边形PQGB为菱形?若存在,试求出BG长;若不存在请说明理由.
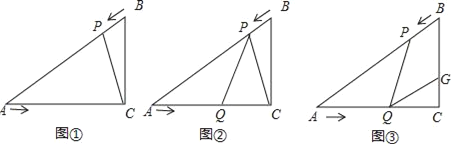
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个工程队需完成A、B两个工地的工程.若甲、乙两个工程队分别可提供40个和50个标准工作量,完成A、B两个工地的工程分别需要70个和20个标准工作量,且两个工程队在A、B两个工地的1个标准工作量的成本如下表所示:
A工地 | B工地 | |
甲工程队 | 800元 | 750元 |
乙工程队 | 600元 | 570元 |
设甲工程队在A工地投入x(20≤x≤40)个标准工作量,完成这两个工程共需成本y元.
(1)求y与x之间的函数关系式;
(2)请判断y是否能等于62000,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,直线![]() 与
与![]() 轴,
轴,![]() 轴分别交于点
轴分别交于点![]() ,点
,点![]() ,对称轴为
,对称轴为![]() 的抛物线过
的抛物线过![]() 两点,且交
两点,且交![]() 轴于另一点
轴于另一点![]() ,连接
,连接![]() .
.
(1)直接写出点![]() ,点
,点![]() ,点
,点![]() 的坐标和抛物线的解析式;
的坐标和抛物线的解析式;
(2)已知点![]() 为第一象限内抛物线上一点,当点
为第一象限内抛物线上一点,当点![]() 到直线
到直线![]() 的距离最大时,求点
的距离最大时,求点![]() 的坐标;
的坐标;
(3)抛物线上是否存在一点![]() (点
(点![]() 除外),使以点
除外),使以点![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出点
相似?若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
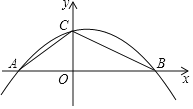
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com