
【题目】镇政府想了解对王家村进行“精准扶贫”一年来村民的经济情况,统计员小李用简单随机抽样的方法,在全村![]() 户家庭中随机抽取
户家庭中随机抽取![]() 户,调查过去一年的收入(单位:万元),从而去估计全村家庭年收入情况.
户,调查过去一年的收入(单位:万元),从而去估计全村家庭年收入情况.
已知调查得到的数据如下:
![]()
![]()
为了便于计算,小李在原数据的每个数上都减去![]() ,得到下面第二组数:
,得到下面第二组数:
![]()
![]()
![]() 请你用小李得到的第二组数计算这
请你用小李得到的第二组数计算这![]() 户家庭的平均年收入,并估计全村年收入及全村家庭年收人超过
户家庭的平均年收入,并估计全村年收入及全村家庭年收人超过![]() 万元的百分比;已知某家庭过去一年的收人是
万元的百分比;已知某家庭过去一年的收人是![]() 万元,请你用调查得到的数据的中位数推测该家庭的收入情况在全村处于什么水平?
万元,请你用调查得到的数据的中位数推测该家庭的收入情况在全村处于什么水平?
![]() 已知小李算得第二组数的方差是
已知小李算得第二组数的方差是![]() ,小王依据第二组数的方差得出原数据的方差为
,小王依据第二组数的方差得出原数据的方差为![]() ,你认为小王的结果正确吗?如果不正确,直接写出你认为正确的结果.
,你认为小王的结果正确吗?如果不正确,直接写出你认为正确的结果.
【答案】(1)见解析;(2)小王的结果不正确.
【解析】
(1)计算出第二组数据的平均数,则把这个平均数加上1.5得到得到这20户家庭的平均年收入;用这20户家庭的平均年收入乘以130可估计全村年收入;用样本中家庭年收人超过1.5万元的百分比表示全村家庭年收人超过1.5万元的百分比,利用中位数的意义判断某家庭过去一年的收人是1.89万元,该家庭的收入情况在全村处于什么水平;
(2)利用方差的意义可判断小王的结果错误,然后根据方差公式计算第二组的方差即可.
解:![]() 第二组数据的平均数为
第二组数据的平均数为![]() ,
,
所以这![]() 户家庭的平均年收入
户家庭的平均年收入![]() (万),
(万),
![]() ,
,
估计全村年收入为![]() 万;
万;
全村家庭年收人超过![]() 万元的百分比为
万元的百分比为![]() ;
;
某家庭过去一年的收人是![]() 万元,则该家庭的收入情况在全村处于中下游;
万元,则该家庭的收入情况在全村处于中下游;
(2)小王的结果不正确.
第一组数据的方差和第二组数据的方差一样.
它们的方差![]() .
.


 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案科目:初中数学 来源: 题型:
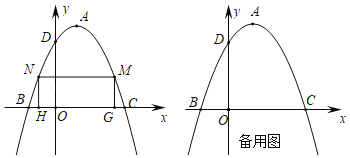
【题目】如图,已知二次函数图象的顶点坐标为![]() ,与坐标轴交于B、C、D三点,且B点的坐标为
,与坐标轴交于B、C、D三点,且B点的坐标为![]() .
.
(1)求二次函数的解析式;
(2)在二次函数图象位于x轴上方部分有两个动点M、N,且点N在点M的左侧,过M、N作x轴的垂线交x轴于点G、H两点,当四边形MNHG为矩形时,求该矩形周长的最大值;
(3)当矩形MNHG的周长最大时,能否在二次函数图象上找到一点P,使![]() 的面积是矩形MNHG面积的
的面积是矩形MNHG面积的![]() ?若存在,求出该点的横坐标;若不存在,请说明理由.
?若存在,求出该点的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,PA、PB为圆O的切线,切点分别为A、B,PO交AB于点C,PO的延长线交圆O于点D,下列结论不一定成立的是( )

A. PA=PBB. ∠BPD=∠APDC. AB⊥PDD. AB平分PD
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司有如图所示的甲、乙、丙、丁四个生产基地.现决定在其中一个基地修建总仓库,以方便公司对各基地生产的产品进行集中存储.已知甲、乙、丙、丁各基地的产量之比等于4:5:4:2,各基地之间的距离之比a:b:c:d:e=2:3:4:3:3(因条件限制,只有图示中的五条运输渠道),当产品的运输数量和运输路程均相等时,所需的运费相等.若要使总运费最低,则修建总仓库的最佳位置为( )
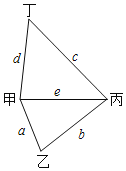
A. 甲B. 乙C. 丙D. 丁
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线经过两点A(﹣3,0),B(0,3),且其对称轴为直线x=﹣1.
(1)求此抛物线的解析式;
(2)若点P是抛物线上点A与点B之间的动点(不包括点A,点B),求△PAB的面积的最大值,并求出此时点P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学数学兴趣小组在一次课外学习与探究中遇到一些新的数学符号,他们将其中某些材料摘录如下:
对于三个实,数![]() ,
,![]() ,
,![]() ,用
,用![]() 表示这三个数的平均数,用
表示这三个数的平均数,用![]() 表示这三个数中最小的数,例如
表示这三个数中最小的数,例如![]()
![]() =4,
=4,![]() ,
,![]() .请结合上述材料,解决下列问题:
.请结合上述材料,解决下列问题:
(1)①![]() _____,
_____,
②![]() _____;
_____;
(2)若![]() ,则
,则![]() 的取值范围为_____;
的取值范围为_____;
(3)若![]() ,求
,求![]() 的值;
的值;
(4)如果![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年3月12日是第41个植树节,某单位积极开展植树活动,决定购买甲、乙两种树苗,用800元购买甲种树苗的棵数与用680元购买乙种树苗的棵数相同,乙种树苗每棵比甲种树苗每棵少6元.
(1)求甲种树苗每棵多少元?
(2)若准备用3800元购买甲、乙两种树苗共100棵,则至少要购买乙种树苗多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
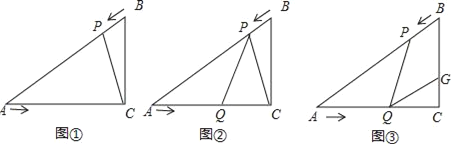
【题目】已知:如图,在Rt△ACB中,∠C=90°,BC=3cm,AC=3![]() cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为
cm,点P由B点出发沿BA方向向点A匀速运动,速度为2cm/s;点Q由A点出发沿AC方向向点C匀速运动,速度为![]() cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题:
cm/s;若设运动的时间为t(s)(0<t<3),解答下列问题:
(1)如图①,连接PC,当t为何值时△APC∽△ACB,并说明理由;
(2)如图②,当点P,Q运动时,是否存在某一时刻t,使得点P在线段QC的垂直平分线上,请说明理由;
(3)如图③,当点P,Q运动时,线段BC上是否存在一点G,使得四边形PQGB为菱形?若存在,试求出BG长;若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
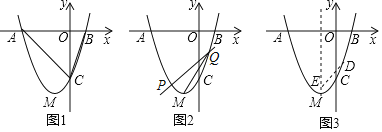
【题目】如图1,抛物线y=ax2+2ax+c与x轴交于A(-3,0)、B两点,与y轴交于C点,△ABC的面积为6,抛物线顶点为M.
(1)如图1,求抛物线的解析式;
(2)如图2,直线y=kx+k-3与抛物线交于P、Q两点(P点在Q点左侧),问在y轴上是否存在点N,使四边形PMQN为矩形?若存在,求N点坐标,若不存在,请说明理由;
(3)如图3,若D为抛物线上任意一点,E(-1,s)为对称轴上一点,若对任意一点D都有ED≥EM,求s的最大值及相应E点坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com