
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
定义:长宽比为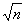 :1(n为正基数)的矩形称为株为
:1(n为正基数)的矩形称为株为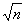 矩形. 下面,我们通过折叠的方式折出一个
矩形. 下面,我们通过折叠的方式折出一个 矩形.
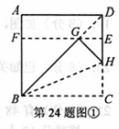
矩形. 如图①所示.
如图①所示.
操作1:将正方形ABCD沿过点B的直线折叠,使折叠后的点C落在对角线BD上的点G处,折痕为BH
操作2:将AD沿过点G的直线折叠,使点A,点D分别落在边AB,CD上,折痕为EF
则四 边形BCEF为
边形BCEF为 矩形
矩形
证明:设正方形ABCD的边长为1,则BD=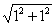 =
= .
.
由折叠性质可知BG=BC=1,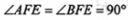 ,则四边形BCEF为矩形
,则四边形BCEF为矩形

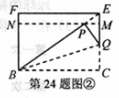
阅读以上内容,回答下列问题:
(1) 在图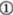 中,所有与CH相等的线段是 ,tan
中,所有与CH相等的线段是 ,tan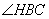 的值是
的值是
(2) 已知四边形BCEF为 矩形,模仿上述操作,得到四边形BCMN,如图
矩形,模仿上述操作,得到四边形BCMN,如图 。
。
求证:四边形BCMN是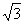 矩形
矩形
将图 中的
中的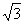 矩形BCM
矩形BCM N沿用(2)中的操作3次后,得到一个“
N沿用(2)中的操作3次后,得到一个“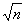 矩形”,则n的值是
矩形”,则n的值是
查看答案和解析>>
科目:初中数学 来源: 题型:
将一副三角尺(在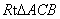 中,∠ACB=
中,∠ACB=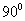 ,∠B=
,∠B=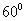 ;在
;在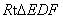 中,∠EDF=
中,∠EDF=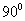 ,∠E=
,∠E= )如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将
)如图摆放,点D为AB的中点,DE交AC于点P,DF经过点C.将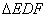 绕点D顺时针方向旋转角
绕点D顺时针方向旋转角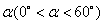 ,
, 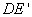 交AC于点M,
交AC于点M,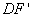 交BC于点N,则
交BC于点N,则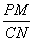 的值为
的值为
A. 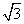 B.
B.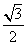 C.
C. 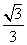 D.
D.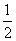
查看答案和解析>>
科目:初中数学 来源: 题型:
在一个三角形中,各边和它所对角的正弦的比相等.即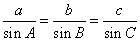 .利用上述结论可以求解如下题目.如:
.利用上述结论可以求解如下题目.如:
在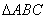 中,若
中,若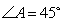 ,
,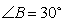 ,
,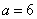 ,求
,求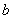 .
.
解:在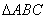 中,
中,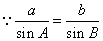
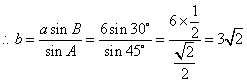
问题解决:
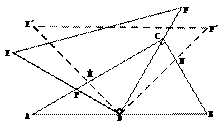
如图,甲船以每小时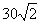 海里的速度向正北方航行,当甲船位于
海里的速度向正北方航行,当甲船位于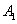 处时,乙船位于甲船的北偏西
处时,乙船位于甲船的北偏西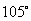 方向的
方向的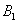 处,且乙船从
处,且乙船从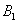 处按北偏东
处按北偏东 方向匀速直线航行,当甲船航行
方向匀速直线航行,当甲船航行 分钟到达
分钟到达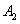 处时,乙船航行到甲船的北偏西
处时,乙船航行到甲船的北偏西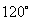 方向的
方向的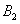 处,此时两船相距
处,此时两船相距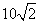 海里.
海里.
(1) 判断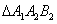 的形状,并给出证明.
的形状,并给出证明.
(2) 乙船每小时航行多少海里?
查看答案和解析>>
科目:初中数学 来源: 题型:
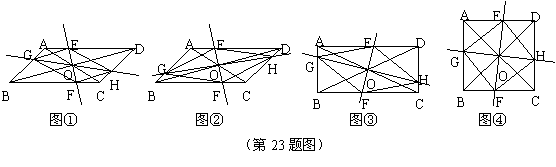
 在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com