
 如图所示,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )
如图所示,AB是⊙O的直径,点D、E是半圆的三等分点,AE、BD的延长线交于点C,若CE=2,则图中阴影部分的面积是( )| A. | $\frac{4}{3}$π-$\sqrt{3}$ | B. | 2π-2$\sqrt{3}$ | C. | $\frac{2}{3}$π-$\sqrt{3}$ | D. | $\frac{1}{3}$π |
分析 已知D、E是半圆的三等分点,如果连接DE、OE、OD,那么△OAE、△ODE、△OBD、△CDE都是等边三角形,由此可求出扇形OBE的圆心角的度数和圆的半径长;由于∠AOE=∠BOD,则AB∥DE,S△ODE=S△BDE;可知阴影部分的面积=S扇形OAE-S△OAE+S扇形ODE求解.
解答 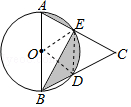 解:连接OE、OD,点D、E是半圆的三等分点,
解:连接OE、OD,点D、E是半圆的三等分点,
∴∠AOE=∠EOD=∠DOB=60°
∵OA=OE=OD=OB
∴△OAE、△ODE、△OBD、△CDE都是等边三角形,
∴AB∥DE,
∴S△ODE=S△BDE;
∴图中阴影部分的面积=S扇形OAE-S△OAE+S扇形ODE=$\frac{60π×{2}^{2}}{360}$×2-$\frac{1}{2}$=$\frac{4}{3}$π-$\sqrt{3}$.
故选:A
点评 本题考查的圆周角定理、三角形的面积及扇形面积公式、等边三角形的判定与性质,关键是将阴影部分面积转化为扇形ODE的面积.


科目:初中数学 来源: 题型:填空题
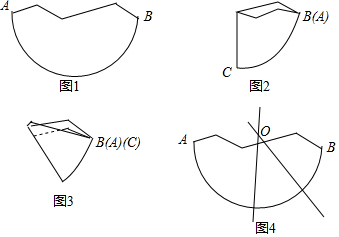 数学课上,老师介绍了利用尺规确定残缺纸片圆心的方法.小华对数学老师说:“我可以用拆叠纸片的方法确定圆心”.小华的作法如下:
数学课上,老师介绍了利用尺规确定残缺纸片圆心的方法.小华对数学老师说:“我可以用拆叠纸片的方法确定圆心”.小华的作法如下:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com