练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

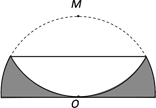
    【题目】如图，一个半径为2的半圆形纸片，按如图方式折叠，使对折后半圆弧的中点M与圆心O重合，则图中阴影部分的面积是

    A.B.－2C.－D.2－

    【答案】D

    【解析】

    连接OM交AB于点C，连接OA、OB，根据题意OM⊥AB且OC=MC=1，继而求出∠AOC=60°、AB=2AC=2 ，然后根据S弓形ABM=S扇形OAB-S△AOB、S阴影=S半圆-2S弓形ABM计算可得答案．

    解：如图，连接OM交AB于点C，连接OA、OB，

    由题意知，OM⊥AB，且OC=MC=1，

    在RT△AOC中，∵OA=2，OC=1，

    ∴cos∠AOC= ，AC=

    ∴∠AOC=60°，AB=2AC=2 ，

    ∴∠AOB=2∠AOC=120°，

    则S弓形ABM=S扇形OAB-S△AOB= ，

    S阴影=S半圆-2S弓形ABM= ．

    故选：D．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

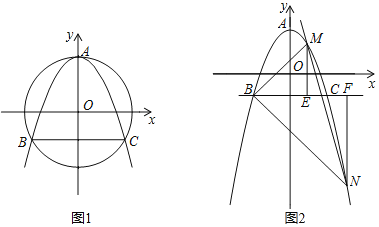
    【题目】已知抛物线y＝ax2+bx+c过顶点A（0，2），以原点O为圆心，OA为半径的圆与抛物线的另两个交点为B，C，且B在C的左侧，△ABC有一个内角为60°．

    （1）求抛物线的解析式.

    （2）若MN与直线y＝﹣2x平行，M（x1，y1），N（x2，y2），M，N都在抛物线上，且M，N位于直线BC的两侧，y1＞y2，ME⊥BC于E，NF⊥BC于F，解决以下问题：

    ①求证：.

    ②求△MBC外心的纵坐标的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

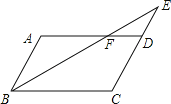
    【题目】如图，平行四边形ABCD中，E是CD的延长线上一点，BE与AD交于点F，CD=2DE．若△DEF的面积为a，则平行四边形ABCD的面积为　 ▲ 　（用a的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】函数图象在探索函数的性质中有非常重要的作用，下面我们就一类特殊的函数展开探索．画函数的图象，经历分析解析式、列表、描点、连线过程得到函数图象如图所示；经历同样的过程画函数和的图象如图所示．

    x

    …

    ﹣3

    ﹣2

    ﹣1

    0

    1

    2

    3

    …

    y

    …

    ﹣6

    ﹣4

    ﹣2

    0

    ﹣2

    ﹣4

    ﹣6

    …

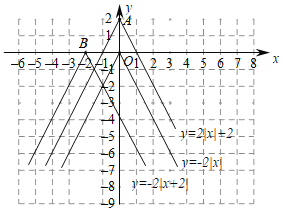
    （1）观察发现：三个函数的图象都是由两条射线组成的轴对称图形；三个函数解折式中绝对值前面的系数相同，则图象的开口方向和形状完全相同，只有最高点和对称轴发生了变化．写出点A，B的坐标和函数的对称轴．

    （2）探索思考：平移函数的图象可以得到函数和的图象，分别写出平移的方向和距离．

    （3）拓展应用：在所给的平面直角坐标系内画出函数的图象．若点和在该函数图象上，且，比较，的大小．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，AB为⊙O的直径，点C为圆上一点，∠BAC＝20°，将劣弧沿弦AC所在的直线翻折，交AB于点D，则弧的度数等于（　　）

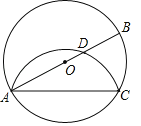
    A.40°B.50C.80°D.100

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】

    （已有经验）

    我们已经研究过作一个圆经过两个已知点，也研究过作一个圆与已知角的两条边都相切，尺规作图如图所示：

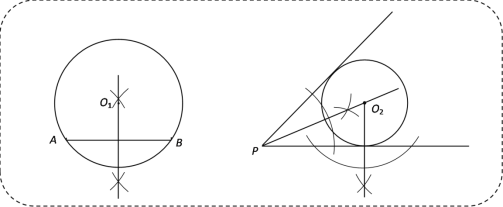
    （迁移经验）

    （1）如图①，已知点M和直线l，用两种不同的方法完成尺规作图：求作⊙O，使⊙O过M点，且与直线l相切．（每种方法作出一个圆即可，保留作图痕迹，不写作法）

    （问题解决）

    如图②，在Rt△ABC中，∠C＝90°，AC＝8，BC＝6．

    （2）已知⊙O经过点C，且与直线AB相切．若圆心O在△ABC的内部，则⊙O半径r的取值范围为 ．

    （3）点D是边AB上一点，BD＝m，请直接写出边AC上使得∠BED为直角时点E的个数及相应的m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形相似但不全等，我们就把这条对角线叫做这个四边形的“相似对角线”.

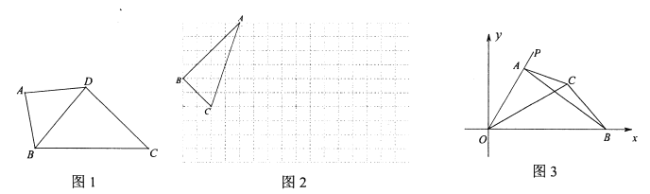
    （1）如图1，在四边形中，，，，对角线平分.求证：是四边形的“相似对角线”；

    （2）如图2，已知格点，请你在正方形网格中画出所有的格点四边形，使四边形是以为“相似对角线”的四边形；（注：顶点在小正方形顶点处的多边形称为格点多边形）

    （3）如图3，四边形中，点在射线：上，点在轴正半轴上，对角线平分，连接.若是四边形的“相似对角线”，，求点的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】建造一个面积为130m2的长方形养鸡场，鸡场的一边靠墙，墙长为a米，另三边用竹篱笆围成，如果篱笆总长为33米．

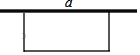
    （1）求养鸡场的长与宽各为多少米？

    （2）若10≤a＜18，题中的解的情况如何？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，已知抛物线．

    (1)求抛物线的对称轴；

    (2)当时，设抛物线与轴交于两点(点在点左侧)，顶点为，若为等边三角形，求的值；

    (3)过(其中)且垂直轴的直线与抛物线交于两点．若对于满足条件的任意值，线段的长都不小于1，结合函数图象，直接写出的取值范围．

    查看答案和解析>>

    同步练习册答案