
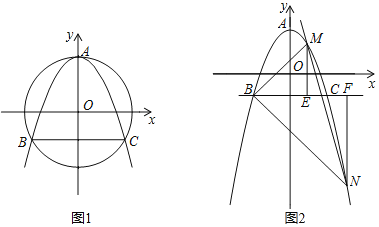
【题目】已知抛物线y=ax2+bx+c过顶点A(0,2),以原点O为圆心,OA为半径的圆与抛物线的另两个交点为B,C,且B在C的左侧,△ABC有一个内角为60°.
(1)求抛物线的解析式.
(2)若MN与直线y=﹣2![]() x平行,M(x1,y1),N(x2,y2),M,N都在抛物线上,且M,N位于直线BC的两侧,y1>y2,ME⊥BC于E,NF⊥BC于F,解决以下问题:
x平行,M(x1,y1),N(x2,y2),M,N都在抛物线上,且M,N位于直线BC的两侧,y1>y2,ME⊥BC于E,NF⊥BC于F,解决以下问题:
①求证:![]() .
.
②求△MBC外心的纵坐标的取值范围.
【答案】(1)抛物线解析式为y=﹣x2+2;(2)①证明见解析;②﹣![]() <y0≤0.
<y0≤0.
【解析】
(1)由顶点坐标为(0,2)可得c=2,由对称轴为y轴可得b=0,△ABC为等腰三角形,根据有一个角是60°可得△ABC是等边三角形,设线段BC与y轴的交点为点D,连接OB,根据垂径定理可得BD=CD,根据外心的定义可得∠OBD=30°,利用∠OBD的正弦和余弦值可求出OD和BD的长,即可得得B坐标,代入抛物线解析式可求出a值,即可得答案;(2)①根据MN与y=﹣2![]() x平行设直线MN的解析式为y=﹣2
x平行设直线MN的解析式为y=﹣2![]() x+m,把M点坐标代入可得m=﹣x12+2
x+m,把M点坐标代入可得m=﹣x12+2![]() x1+2,即可得出MN的解析式,代入y=﹣x2+2可用x1表示出x2,进而可表示出y2,分别用x1表示出∠MBE和∠NBF的正切函数即可得结论;②过M作ME⊥y轴于E,由y轴为BC的垂直平分线,可知△NBC的外心在y轴上,设外心P坐标为(0,y0),可得PB=PM,利用勾股定理可用y1表示出y0,根据y1的取值范围即可得答案.
x1+2,即可得出MN的解析式,代入y=﹣x2+2可用x1表示出x2,进而可表示出y2,分别用x1表示出∠MBE和∠NBF的正切函数即可得结论;②过M作ME⊥y轴于E,由y轴为BC的垂直平分线,可知△NBC的外心在y轴上,设外心P坐标为(0,y0),可得PB=PM,利用勾股定理可用y1表示出y0,根据y1的取值范围即可得答案.
(1)∵抛物线过点A(0,2),
∴c=2,
∴抛物线的对称轴为y轴,且开口向下,即b=0,
∵以O为圆心,OA为半径的圆与抛物线交于另两点B,C,y轴为抛物线对称轴,
∴B、C关于y轴对称,
∴△ABC为等腰三角形,
∵△ABC中有一个角为60°,
∴△ABC为等边三角形,且OC=OA=2,
设线段BC与y轴的交点为点D,连接OB,
∵AD⊥BC,AD过圆心,
∴BD=CD,
∵O为△ABC的外心,△ABC为等边三角形,
∴∠OBD=30°,
∴BD=OBcos30°=![]() ,OD=OBsin30°=1,
,OD=OBsin30°=1,
∵B在C的左侧,
∴B的坐标为(﹣![]() ,﹣1),
,﹣1),
∵B点在抛物线上,且c=2,b=0,
∴3a+2=﹣1,
解得:a=﹣1,
则抛物线解析式为y=﹣x2+2.
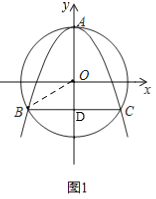
(2)①由(1)知,点M(x1,﹣x12+2),N(x2,﹣x22+2),
∵MN与直线y=﹣2![]() x平行,
x平行,
∴设直线MN的解析式为y=﹣2![]() x+m,
x+m,
∴﹣x12+2=﹣2![]() x1+m,即m=﹣x12+2
x1+m,即m=﹣x12+2![]() x1+2,
x1+2,
∴直线MN解析式为y=﹣2![]() x﹣x12+2
x﹣x12+2![]() x1+2,
x1+2,
把y=﹣2![]() x﹣x12+2
x﹣x12+2![]() x1+2代入y=﹣x2+2,
x1+2代入y=﹣x2+2,
解得:x=x1或x=2![]() ﹣x1,
﹣x1,
∴x2=2![]() ﹣x1,即y2=﹣(2
﹣x1,即y2=﹣(2![]() ﹣x1)2+2=﹣x12+4
﹣x1)2+2=﹣x12+4![]() x1﹣10,
x1﹣10,
如图2所示,作ME⊥BC,NF⊥BC,垂足为E,F,
∵M,N位于直线BC的两侧,且y1>y2,
∴y2<﹣1<y1≤2,且﹣![]() <x1<x2,
<x1<x2,
∴ME=y1﹣(﹣1)=﹣x12+3,BE=x1﹣(﹣![]() )=x1+
)=x1+![]() ,
,
NF=﹣1﹣y2=x12﹣4![]() x1+9,BF=x2﹣(﹣
x1+9,BF=x2﹣(﹣![]() )=3
)=3![]() ﹣x1,
﹣x1,
在Rt△BEM中,tan∠MBE=![]() =
=![]() =
=![]() ﹣x1,
﹣x1,
在Rt△BFN中,tan∠NBF=![]() =
=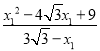
=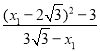
=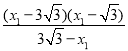
=![]() -x1,
-x1,
∴![]() =
=![]() .
.
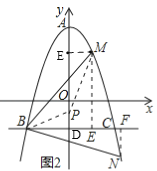
②过M作ME⊥y轴于E,
∵y轴为BC的垂直平分线,
∴设△MBC的外心为P(0,y0),则PB=PM,即PB2=PM2,
∵B的坐标为(﹣![]() ,﹣1),
,﹣1),
∴PD=y0+1,PD=![]() ,ME=x1,PE=y1﹣y0,
,ME=x1,PE=y1﹣y0,
根据勾股定理得:3+(y0+1)2=x12+(y1﹣y0)2,
∵x12=2﹣y1,
∴y02+2y0+4=(2﹣y1)+(y0﹣y1)2,即y0=![]() y1﹣1,
y1﹣1,
由①得:﹣1<y1≤2,
∴﹣![]() <y0≤0,
<y0≤0,
则△MBC的外心的纵坐标的取值范围是﹣![]() <y0≤0.
<y0≤0.


 春雨教育同步作文系列答案
春雨教育同步作文系列答案科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0.
(1)当方程有一个根为﹣1时,求k的值及另一个根;
(2)当方程有两个不相等的实数根,求k的取值范围;
(3)若方程两实根x1、x2满足x1+x2=x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
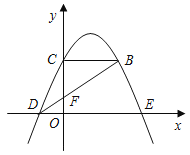
【题目】如图,抛物线y=﹣![]() (x﹣k)2+
(x﹣k)2+![]() 经过点D(﹣1,0),与x轴正半轴交于点E,与y轴交于点C,过点C作CB∥x轴交抛物线于点B.连接BD交y轴于点F.
经过点D(﹣1,0),与x轴正半轴交于点E,与y轴交于点C,过点C作CB∥x轴交抛物线于点B.连接BD交y轴于点F.
(1)求点E的坐标.
(2)求△CFB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
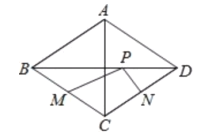
【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的中点,P是线段BD上的一个动点,则PM+PN的最小值是( )
A.![]() B.3
B.3
C.![]() D.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】设二次函数y1=ax2+bx+a﹣5(a,b为常数,a≠0),且2a+b=3.
(1)若该二次函数的图象过点(﹣1,4),求该二次函数的表达式;
(2)y1的图象始终经过一个定点,若一次函数y2=kx+b(k为常数,k≠0)的图象也经过这个定点,探究实数k,a满足的关系式;
(3)已知点P(x0,m)和Q(1,n)都在函数y1的图象上,若x0<1,且m>n,求x0的取值范围(用含a的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们县是紫菜生产大县,某景点商户向游客推销一种加工好的优质紫菜,已知每千克成本为20元.市场调查发现,在一段时间内,该产品销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)的变化而变化有如下关系式:
(元/千克)的变化而变化有如下关系式:![]() .设这种紫菜在这段时间内的销售利润为
.设这种紫菜在这段时间内的销售利润为![]() (元).
(元).
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定该景区这种紫菜的销售单价不得高于28元/千克,该商户每天能否获得比150元更大的利润?如果能请求出最大利润,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.圆内接正六边形的边长与该圆的半径相等
B.在平面直角坐标系中,不同的坐标可以表示同一点
C.一元二次方程ax2+bx+c=0(a≠0)一定有实数根
D.将△ABC绕A点按顺时针方向旋转60°得△ADE,则△ABC与△ADE不全等
查看答案和解析>>
科目:初中数学 来源: 题型:
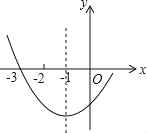
【题目】如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=﹣1,且过点(﹣3,0),下列说法:
①b2﹣4ac=0;
②4a+2b+c<0;
③3a+c=0;
④若(﹣5,y1),(2,y2)是抛物线上的两点,则y1>y2,
其中正确的是( )
A.1个 B.2个 C.3个 D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com