
����Ŀ�����������ϲ��������أ�ij�����̻����ο�����һ�ּӹ��õ������ϲˣ���֪ÿǧ�˳ɱ�Ϊ20Ԫ.�г����鷢�֣���һ��ʱ���ڣ��ò�Ʒ������![]() ��ǧ�ˣ������۵���
��ǧ�ˣ������۵���![]() ��Ԫ/ǧ�ˣ��ı仯���仯�����¹�ϵʽ��
��Ԫ/ǧ�ˣ��ı仯���仯�����¹�ϵʽ��![]() .�������ϲ������ʱ���ڵ���������Ϊ
.�������ϲ������ʱ���ڵ���������Ϊ![]() ��Ԫ��.
��Ԫ��.
��1����![]() ��
��![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��2�������ۼ۶�Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
��3�������۲��Ź涨�þ��������ϲ˵����۵��۲��ø���28Ԫ/ǧ�ˣ����̻�ÿ���ܷ��ñ�150Ԫ��������������������������������ܣ���˵������.
���𰸡���1��y![]() ;��2�������ۼ۶�Ϊ30Ԫʱ��ÿ�����������������������200Ԫ;��3���ܣ������ۼ۶�Ϊ28Ԫʱ��ÿ��������������ʱ
;��2�������ۼ۶�Ϊ30Ԫʱ��ÿ�����������������������200Ԫ;��3���ܣ������ۼ۶�Ϊ28Ԫʱ��ÿ��������������ʱ![]() Ԫ�������̻�ÿ���ܻ�ñ�150Ԫ���������.
Ԫ�������̻�ÿ���ܻ�ñ�150Ԫ���������.
��������
��1����������=���ۼ�-�ɱ��������������������![]() ��
��![]() �Ĺ�ϵʽ��
�Ĺ�ϵʽ��
��2���ɣ�1���еĶ��κ�������˶��κ��������ֵ���ɵõ��������
��3���ɣ�1���еĶ��κ����õ������ԣ����������Կ����![]() ʱ���������ֵ.
ʱ���������ֵ.
�⣺��1��![]()
![]() .
.
��2��![]()
���Ե����ۼ۶�Ϊ30Ԫʱ��ÿ�����������������������200Ԫ.
��3����![]() ������
������![]() ��
��
����![]() ʱ��
ʱ��![]() ��
��![]() �����������
�����������
����![]() ʱ��
ʱ��![]() ��
��![]() �����������.
�����������.
���ԣ������ۼ۶�Ϊ28Ԫʱ��ÿ��������������ʱ![]() Ԫ�������̻�ÿ���ܻ�ñ�150Ԫ���������.
Ԫ�������̻�ÿ���ܻ�ñ�150Ԫ���������.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڰ뾶Ϊ6����O�У���������ABCDEF��������AGDH���ڽ�����O����ͼ����Ӱ���ֵ����Ϊ��������

A. 27��9![]() B. 18
B. 18![]() C. 54��18
C. 54��18![]() D. 54
D. 54
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
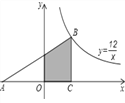
����Ŀ����ͼ��Rt��ABC�Ķ���B�ڷ���������![]() ��ͼ���ϣ�AC����x���ϣ���֪��ACB=90�㣬��A=30�㣬BC=4����ͼ����Ӱ���ֵ������_________
��ͼ���ϣ�AC����x���ϣ���֪��ACB=90�㣬��A=30�㣬BC=4����ͼ����Ӱ���ֵ������_________
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����O�е���BC���ڡ�O�İ뾶���ӳ�BC��D��ʹBC��CD����AΪ�Ż�BC�ϵ�һ�����㣬����AD��AB��AC������D��DE��AB����ֱ��AB�ڵ�E������A���Ż�BC�ϴӵ�C�˶�����Bʱ����DE+AC��ֵ�ı仯����ǣ� ��
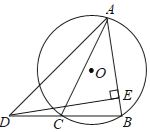
A.����B.�ȱ���ٱ�СC.�ȱ�С�ٱ��D.��ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
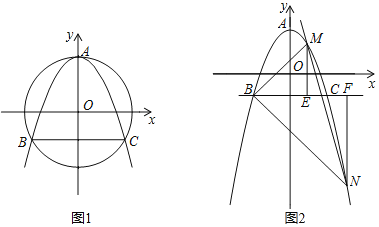
����Ŀ����֪������y��ax2+bx+c������A��0��2������ԭ��OΪԲ�ģ�OAΪ�뾶��Բ�������ߵ�����������ΪB��C����B��C����࣬��ABC��һ���ڽ�Ϊ60����
��1���������ߵĽ���ʽ.
��2����MN��ֱ��y����2![]() xƽ�У�M��x1��y1����N��x2��y2����M��N�����������ϣ���M��Nλ��ֱ��BC�����࣬y1��y2��ME��BC��E��NF��BC��F������������⣺
xƽ�У�M��x1��y1����N��x2��y2����M��N�����������ϣ���M��Nλ��ֱ��BC�����࣬y1��y2��ME��BC��E��NF��BC��F������������⣺
����֤��![]() .
.
�����MBC���ĵ��������ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������![]() �����ķ�չ�����ǶԸ���
�����ķ�չ�����ǶԸ���![]() ��Ʒ��ʹ�ó����ڴ�.ij��˾�ƻ���ij�������۵�һ��
��Ʒ��ʹ�ó����ڴ�.ij��˾�ƻ���ij�������۵�һ��![]() ��Ʒ�������г��������ò�Ʒ�����ۼ۸����������ڵı仯���仯.��ò�Ʒ�ڵ�
��Ʒ�������г��������ò�Ʒ�����ۼ۸����������ڵı仯���仯.��ò�Ʒ�ڵ�![]() ��
��![]() Ϊ������������������ÿ̨�����ۼ۸�Ϊ
Ϊ������������������ÿ̨�����ۼ۸�Ϊ![]() Ԫ��
Ԫ��![]() ��
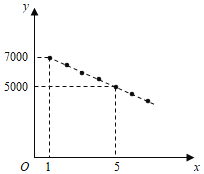
��![]() ֮��������ͼ��ʾ��һ�κ�����ϵ.
֮��������ͼ��ʾ��һ�κ�����ϵ.
��1����![]() ��
��![]() ֮��Ĺ�ϵʽ��
֮��Ĺ�ϵʽ��
��2����ò�Ʒ�ڵ�![]() ���������ڵ���������Ϊ
���������ڵ���������Ϊ![]() ����̨����
����̨����![]() ��
��![]() �Ĺ�ϵ����
�Ĺ�ϵ����![]() ������������������Ϣ�����ʣ��ĸ��������ڵ������������ʱ�ò�Ʒÿ̨�����ۼ۸��Ƕ���Ԫ��
������������������Ϣ�����ʣ��ĸ��������ڵ������������ʱ�ò�Ʒÿ̨�����ۼ۸��Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������������һ����ABC������ã�2��1����ʾ����ֽ��A���λ�ã���1��2����ʾB���λ�ã�C��Ķ���Ҳ��������ϣ�
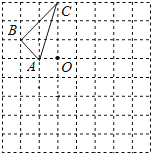
��1��������ABC���ڵ�O�ĶԳ�ͼ����A��B��C������д��������Ҫ��ͼ�б����ĸ����
��2��д��A����B����C����������ꣻ
��3���������ϵ���С�����α߳�Ϊ1�������A���BC���������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
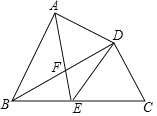
����Ŀ����ͼ�����ı���ABCD�У��Խ���BDƽ��![]() ��
��![]() ��EΪBC���е㣬AE��BD�ཻ�ڵ�F����
��EΪBC���е㣬AE��BD�ཻ�ڵ�F����![]() ����BF�ij�Ϊ�� ��
����BF�ij��� ��
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��
�����о��飩
�����Ѿ��о�����һ��Բ����������֪�㣬Ҳ�о�����һ��Բ����֪�ǵ������߶����У��߹���ͼ��ͼ��ʾ��
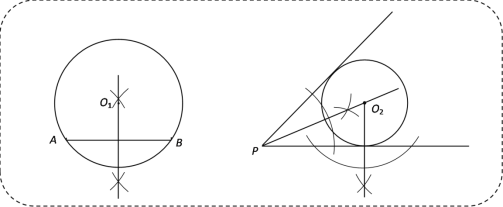
��Ǩ�ƾ��飩
��1����ͼ�٣���֪��M��ֱ��l�������ֲ�ͬ�ķ�����ɳ߹���ͼ��������O��ʹ��O��M�㣬����ֱ��l���У���ÿ�ַ�������һ��Բ���ɣ�������ͼ�ۼ�����д������

����������
��ͼ�ڣ���Rt��ABC�У���C��90����AC��8��BC��6��
��2����֪��O������C������ֱ��AB���У���Բ��O����ABC���ڲ������O�뾶r��ȡֵ��ΧΪ ��
��3����D�DZ�AB��һ�㣬BD��m����ֱ��д����AC��ʹ�á�BEDΪֱ��ʱ��E�ĸ�������Ӧ��m��ȡֵ��Χ��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com