
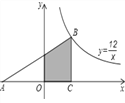
【题目】如图,Rt△ABC的顶点B在反比例函数![]() 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是_________
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是_________
科目:初中数学 来源: 题型:
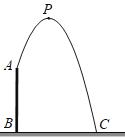
【题目】如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2.25m,喷出水流的运动路线是抛物线.水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3m.求水流的落地点C到水枪底部B的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈尔滨市滑雪业提前进入旺季,某体育用品商店购进一批简易滑雪板,每件进价为100元,售价为130元,每星期可卖出80件.商家决定降价促销,根据市场调查,每降价5元,每星期可多卖出20件.
(1)设商家每件售价x元,每星期的销售数量为y元,求y与x之间的函数关系式;
(2)降价后,商家要使每星期的销售利润W最大,应将售价定为多少元?最大销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,以BC为弦的⊙O分别与AB,AC交于点D和E,点F是BC延长线上一点,CF=AE,连接EF.
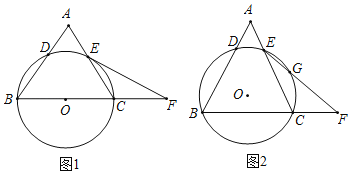
(1)如图1,BC为直径,求证:EF是⊙O的切线;
(2)如图2,EF与⊙O交于点G,⊙O的半径为1,BC的长为![]() π,求BF的长.
π,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
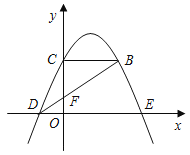
【题目】如图,抛物线y=﹣![]() (x﹣k)2+
(x﹣k)2+![]() 经过点D(﹣1,0),与x轴正半轴交于点E,与y轴交于点C,过点C作CB∥x轴交抛物线于点B.连接BD交y轴于点F.
经过点D(﹣1,0),与x轴正半轴交于点E,与y轴交于点C,过点C作CB∥x轴交抛物线于点B.连接BD交y轴于点F.
(1)求点E的坐标.
(2)求△CFB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】书法是我国的文化瑰宝,研习书法能培养高雅的品格.某校为加强书法教学,了解学生现有的书写能力,随机抽取了部分学生进行测试,测试结果分为优秀、良好、及格、不及格四个等级,分别用A,B,C,D表示,并将测试结果绘制成如图两幅不完整的统计图.

请根据统计图中的信息解答以下问题:
(1)本次抽取的学生人数是 ,扇形统计图中A所对应扇形圆心角的度数是 .
(2)把条形统计图补充完整.
(3)若该学校共有2800人,等级达到优秀的人数大约有多少?
(4)A等级的4名学生中有3名女生1名男生,现在需要从这4人中随机抽取2人参加电视台举办的“中学生书法比赛”,请用列表或画树状图的方法,求被抽取的2人恰好是1名男生1名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
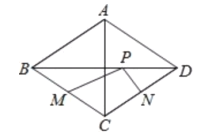
【题目】如图,菱形ABCD中,对角线AC=6,BD=8,M、N分别是BC、CD上的中点,P是线段BD上的一个动点,则PM+PN的最小值是( )
A.![]() B.3
B.3
C.![]() D.5
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们县是紫菜生产大县,某景点商户向游客推销一种加工好的优质紫菜,已知每千克成本为20元.市场调查发现,在一段时间内,该产品销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)的变化而变化有如下关系式:
(元/千克)的变化而变化有如下关系式:![]() .设这种紫菜在这段时间内的销售利润为
.设这种紫菜在这段时间内的销售利润为![]() (元).
(元).
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定该景区这种紫菜的销售单价不得高于28元/千克,该商户每天能否获得比150元更大的利润?如果能请求出最大利润,如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店经销一种健身球,已知这种健身球的成本价为每个20元,市场调查发现,该种健身球每天的销售量y(个)与销售单价x(元)有如下关系:y=﹣20x+80(20≤x≤40),设这种健身球每天的销售利润为w元.
(1)求w与x之间的函数关系式;
(2)该种健身球销售单价定为多少元时,每天的销售利润最大?最大利润是多少元?
(3)如果物价部门规定这种健身球的销售单价不高于28元,该商店销售这种健身球每天要获得150元的销售利润,销售单价应定为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com