
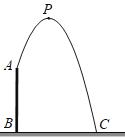
【题目】如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2.25m,喷出水流的运动路线是抛物线.水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3m.求水流的落地点C到水枪底部B的距离.
【答案】水流的落地点C到水枪底部B的距离为3m.
【解析】
如图,以点B为原点,AB为y轴,BC为x轴建立平面直角坐标系,根据点P到x轴、y轴的距离可得点P坐标,设抛物线的解析式为y=a(x﹣1)2+3,把A点坐标代入可求出a值,可得抛物线的解析式,把y=0代入求出x的值即可得答案.
如图,以点B为原点,AB为y轴,BC为x轴建立平面直角坐标系
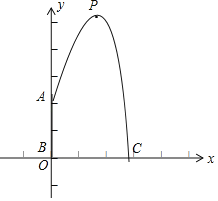
∵最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3m.
∴抛物线的顶点P(1,3)
∴设抛物线的解析式为y=a(x﹣1)2+3,
∵A(0,2.25)
∴a(0-1)2+3=2.25,
解得:a=﹣0.75
∴y=﹣0.75(x﹣1)2+3
令y=0
﹣0.75(x﹣1)2+3=0
解得x1=3,x2=﹣1(舍)
∴BC=3.
答:水流的落地点C到水枪底部B的距离为3m.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E为AD边上的一点,过C点作CF⊥CE交AB的延长线于点F.
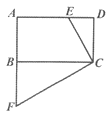
(1)求证:△CDE∽△CBF;
(2)若B为AF的中点,CB=3,DE=1,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(-1,0)、B(4,0)、C(0,2)三点.
(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2,求S1-S2的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,∠A=30°,AC的垂直平分线交AC边于点D,交AB边于点O,以点O为圆心,OB的长为半径作圆,与AB边交于点E.
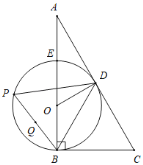
(1)求证:AC是⊙O的切线;
(2)若点P为⊙O上的动点(含点E,B),连接BD、BP、DP.
①当点P只在BE左侧半圆上时,如果BC∥DP,求∠BDP的度数;
②若Q是BP的中点,当BE=4时,直接写出CQ长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
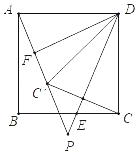
【题目】如图,在正方形ABCD中,E是边BC上的一动点(不与点B、C重合),连接DE、点C关于直线DE的对称点为C′,连接AC′并延长交直线DE于点P,F是AC′的中点,连接DF.
(1)求∠FDP的度数;
(2)连接BP,请用等式表示AP、BP、DP三条线段之间的数量关系,并证明;
(3)连接AC,若正方形的边长为![]() ,请直接写出△ACC′的面积最大值.
,请直接写出△ACC′的面积最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.
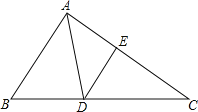
(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,现给出以下四个结论:(1)AE=CF;(2)△EPF是等腰直角三角形;(3)S四边形AEPF=![]() S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )
S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )

A.1个B.3个C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为6的⊙O中,正六边形ABCDEF与正方形AGDH都内接于⊙O,则图中阴影部分的面积为( )

A. 27﹣9![]() B. 18
B. 18![]() C. 54﹣18
C. 54﹣18![]() D. 54
D. 54
查看答案和解析>>
科目:初中数学 来源: 题型:
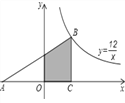
【题目】如图,Rt△ABC的顶点B在反比例函数![]() 的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是_________
的图象上,AC边在x轴上,已知∠ACB=90°,∠A=30°,BC=4,则图中阴影部分的面积是_________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com