
【题目】如图,Rt△ABC中,∠ABC=90°,∠A=30°,AC的垂直平分线交AC边于点D,交AB边于点O,以点O为圆心,OB的长为半径作圆,与AB边交于点E.
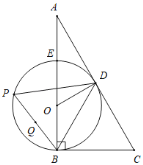
(1)求证:AC是⊙O的切线;
(2)若点P为⊙O上的动点(含点E,B),连接BD、BP、DP.
①当点P只在BE左侧半圆上时,如果BC∥DP,求∠BDP的度数;
②若Q是BP的中点,当BE=4时,直接写出CQ长度的最小值.
【答案】(1)见解析;(2)①60°,②![]()
【解析】
(1)连接OC,证明△ODC≌△OBC,说明OD=OB,即可完成证明.
(2)①根据平行线的性质即可解答
②如图2中,连接OP,取OB的中点J,连接JQ,求出JQ,JC,根据CQ≥JC-JQ即可解决问题.
(1)证明:如图1中,连接OC.
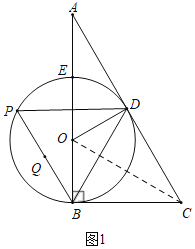
∵∠ABC=90°,∠A=30°,
∴∠ACB=60°,
∵OD垂直平分线段AC,
∴OA=OC,
∴∠A=∠OCA=30°,
∴∠OCB=∠OCD=30°,
∵∠ODC=∠OBC=90°,OC=OC,
∴△ODC≌△OBC(AAS),
∴OD=OB,
∴AC是⊙O的切线.
(2)①解:如图1中,∵DP∥BC,
∴∠PDB=∠DBC,
∵∠ABC=90°,AD=DC,
∴BD=DC=AD,
∵∠DCB=60°,
∴△BDC是等边三角形,
∴∠DBC=60°,
∴∠BDP=60°.
②解:如图2中,连接OP,取OB的中点J,连接JQ.
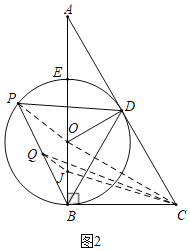
∵BE=4,
∴OB=OE=OD=OP=2,JO=JB=1,
∵∠OBC=90°,∠OCB=30°,
∴BC=![]() OB=2
OB=2![]() ,
,
∴JC=![]() =
=![]() =
=![]() ,
,
∵QP=QB,JO=JB,
∴JQ=![]() OP=1,
OP=1,
∵CQ≥JC﹣JQ,
∴CQ≥![]() ﹣1,
﹣1,
∴CQ的最小值为![]() ﹣1.
﹣1.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
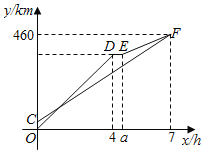
【题目】甲、乙两车从A地出发,沿同一路线驶向B地.甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地.甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60km/h;③乙出发80min追上甲;④乙刚到达货站时,甲距B地180km.其中正确是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某保健品厂每天生产A,B两种品牌的保健品共600瓶,A,B两种产品每瓶的成本和售价如下表,设每天生产A产品x瓶,生产这两种产品每天共获利y元.
A | B | |
成本(元)/瓶 | 50 | 35 |
售价(元)/瓶 | 70 | 50 |
(1)请求出y关于x的函数关系;
(2)该厂每天生产的A,B两种产品被某经销商全部订购,厂家对B产品不变,对A产品进行让利,每瓶利润降低![]() 元,厂家如何生产可使每天获利最大?最大利润是多少?
元,厂家如何生产可使每天获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
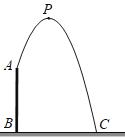
【题目】如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2.25m,喷出水流的运动路线是抛物线.水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3m.求水流的落地点C到水枪底部B的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一堂数学实践课上,赵老师给出了下列问题:
(提出问题)
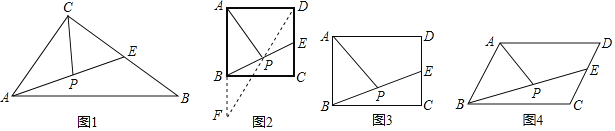
(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=90°,AC=3,AB=5.则CP= .
(探究规律)
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”,若AB=4.则AP的长为 (按图示辅助线求解);
(3)在图3中,AP是矩形ABCD的“双中线”,若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
(拓展应用)
(4)在图4中,AP是平行四边形ABCD的“双中线”,若AB=4,BC=10,∠BAD=120°.求出△ABP的周长,并说明理由?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,以BC为弦的⊙O分别与AB,AC交于点D和E,点F是BC延长线上一点,CF=AE,连接EF.
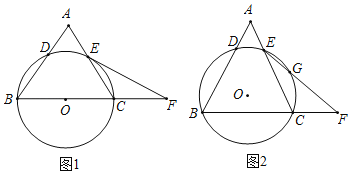
(1)如图1,BC为直径,求证:EF是⊙O的切线;
(2)如图2,EF与⊙O交于点G,⊙O的半径为1,BC的长为![]() π,求BF的长.
π,求BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com