
����Ŀ��ij����Ʒ��ÿ������A��B����Ʒ�Ƶı���Ʒ��600ƿ��A��B���ֲ�Ʒÿƿ�ijɱ����ۼ����±�����ÿ������A��Ʒxƿ�����������ֲ�Ʒÿ�칲����yԪ��
A | ��B | |
�ɱ���Ԫ��/ƿ | 50 | ��35 |
�ۼۣ�Ԫ��/ƿ | 70 | ������50 |
��1�������y����x�ĺ�����ϵ��
��2���ó�ÿ��������A��B���ֲ�Ʒ��ij������ȫ�����������Ҷ�B��Ʒ���䣬��A��Ʒ����������ÿƿ����![]() Ԫ���������������ʹÿ����������������Ƕ��٣�
Ԫ���������������ʹÿ����������������Ƕ��٣�
���𰸡���1��y����x�ĺ�����ϵΪ��y��5x+9000����2��ÿ������A��Ʒ250����B��Ʒ350����������������Ϊ9625Ԫ��
��������
��1���������⣬���ɵ�y����x�ĺ�����ϵʽΪ��y����70��50��x+��50��35����600��x����Ȼ����ô𰸣�
��2�����ȱ�ʾ��������x֮��Ĺ�ϵ�����ó�������ֵ��
��1��������ã�
y����70��50��x+��50��35����600��x��
��5x+9000
��y����x�ĺ�����ϵΪ��y��5x+9000��
��2��������ã�
y����70��50��![]() ��x+��50��35����600��x��
��x+��50��35����600��x��
����![]() ��x��250��2+9625
��x��250��2+9625
�ߩ�![]() ��0
��0
�൱x��250ʱ��y�����ֵ9625
��ÿ������A��Ʒ250����B��Ʒ350����������������Ϊ9625Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У���B=��C��FΪBC���е㣬D��E�ֱ�Ϊ��AB��AC�ϵĵ㣬�ҡ�ADF=��AEF.
�У���B=��C��FΪBC���е㣬D��E�ֱ�Ϊ��AB��AC�ϵĵ㣬�ҡ�ADF=��AEF.
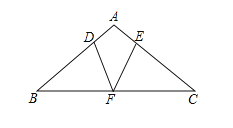
(1)��֤:��BDF����CEF.
(2)����A= 100�㣬BD=BFʱ�����DFE�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ת����ָ������ÿ�������ϵĻ�����ȣ���ͬʱת��![]() ��
��![]() ����ת�̣�ֹͣ��ָ���ָ��һ�����֣�С�Ϻ�С������������ת������Ϸ��������֮��Ϊ��������С��ʤ������С��ʤ������Ϊ�����Ϸ��ƽ��?�������ƽ����˭������������������״ͼ���б���˵�����ɣ�
����ת�̣�ֹͣ��ָ���ָ��һ�����֣�С�Ϻ�С������������ת������Ϸ��������֮��Ϊ��������С��ʤ������С��ʤ������Ϊ�����Ϸ��ƽ��?�������ƽ����˭������������������״ͼ���б���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪���κ���y=ax2+bx+c��a��0����ͼ��A��-1��0����B��4��0����C��0��2�����㣮
��1����ö��κ����Ľ���ʽ��
��2����D�Ǹö��κ���ͼ���ϵ�һ�㣬�������DBA=��CAO��O������ԭ�㣩�����D�����ꣻ
��3����P�Ǹö��κ���ͼ����λ��һ�����ϵ�һ���㣬����PA�ֱ�BC��y�����E��F������PEB����CEF������ֱ�ΪS1��S2����S1-S2�����ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������κ���y��x2��5x��6��x���Ϸ���ͼ����x�ᷭ�۵�x���·���ͼ������ಿ�ֲ��䣬�õ�һ����ͼ����ֱ��y��2x+b�������ͼ����3�������㣬��b��ֵΪ��������
A. ��![]() ��12B. ��
��12B. ��![]() ��2C. ��12��2D. ��
��2C. ��12��2D. ��![]() ��12
��12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���ABC��90������A��30����AC�Ĵ�ֱƽ���߽�AC���ڵ�D����AB���ڵ�O���Ե�OΪԲ�ģ�OB�ij�Ϊ�뾶��Բ����AB�߽��ڵ�E��
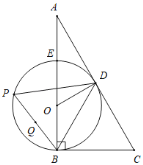
��1����֤��AC�ǡ�O�����ߣ�
��2������PΪ��O�ϵĶ��㣨����E��B��������BD��BP��DP��
�ٵ���Pֻ��BE����Բ��ʱ�����BC��DP�����BDP�Ķ�����
����Q��BP���е㣬��BE��4ʱ��ֱ��д��CQ���ȵ���Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
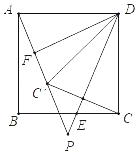
����Ŀ����ͼ����������ABCD�У�E�DZ�BC�ϵ�һ���㣨�����B��C�غϣ�������DE����C����ֱ��DE�ĶԳƵ�ΪC�䣬����AC�䲢�ӳ���ֱ��DE�ڵ�P��F��AC����е㣬����DF��
��1�����FDP�Ķ�����
��2������BP�����õ�ʽ��ʾAP��BP��DP�����߶�֮���������ϵ����֤����
��3������AC���������εı߳�Ϊ![]() ����ֱ��д����ACC���������ֵ��
����ֱ��д����ACC���������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB��AC����BAC��90����ֱ�ǡ�EPF�Ķ���P��BC���е㣬����PE��PF�ֱ�AB��AC�ڵ�E��F���ָ��������ĸ����ۣ���1��AE��CF����2����EPF�ǵ���ֱ�������Σ���3��S�ı���AEPF��![]() S��ABC����4������EPF����ABC���ƶ���P��תʱʼ����EF��AP������E����A��B�غϣ�����������������ȷ�Ľ��۵ĸ����ǣ�������
S��ABC����4������EPF����ABC���ƶ���P��תʱʼ����EF��AP������E����A��B�غϣ�����������������ȷ�Ľ��۵ĸ����ǣ�������

A.1��B.3��C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڱ߳�Ϊ1����������ɵ������У���AOB�Ķ�����ڸ���ϣ����е�A��5��4����B��1��3��������AOB�Ƶ�O��ʱ����ת90���õ���A1OB1��

��1��������A1OB1��
��2��������ת�������߶�AB��BOɨ����ͼ�ε����֮�ͣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com