练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，是⊙的直径，点D是弧AC的中点，∠COD＝60°.

    ⑴三角形AOD是等边三角形吗？请说明理由；

    ⑵求证：OD∥BC .

    【答案】（1）是，理由见解析（2）证明见解析.

    【解析】

    （1）根据弧、圆心角、弦之间的关系定理得到∠AOD=∠COD＝60°，即可得到三角形AOD是等边三角形；

    （2）证明△COB为等边三角形，得到∠AOD=∠OBC＝60°，即可求解.

    三角形AOD是等边三角形，证明如下：

    ∵点D是弧AC的中点，

    ∴∠AOD=∠COD＝60°

    ∵AO=DO,

    ∴三角形AOD是等边三角形；

    （2）∵是⊙的直径，∠AOD=∠COD＝60°

    ∴∠COB＝180°-∠AOD-∠COD= 60°

    又OC=OB，

    △COB为等边三角形，

    ∴∠AOD=∠OBC＝60°，

    故OD∥BC .

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】顺次连接一个四边形的各边中点，得到了一个矩形，则下列四边形中满足条件的是（　　）

    ①平行四边形；②菱形；③矩形；④对角线互相垂直的四边形．

    A. ①③B. ②③C. ③④D. ②④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

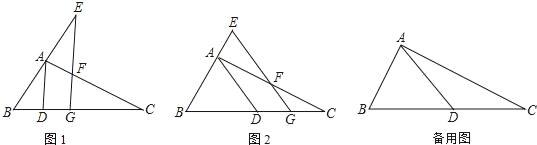
    【题目】如图，Rt△ABC中，∠BAC＝90°，AB＝2，AC＝4，D是BC边上一动点，G是BC边上的一动点，GE∥AD分别交AC、BA或其延长线于F、E两点

    （1）如图1，当BC＝5BD时，求证：EG⊥BC；

    （2）如图2，当BD＝CD时，FG+EG是否发生变化？证明你的结论；

    （3）当BD＝CD，FG＝2EF时，DG的值＝　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】水库90天内的日捕捞量y（kg）与时间第x（天）满足一次函数的关系，部分数据如表：

    时间第x（天）

    1

    3

    6

    10

    日捕捞量（kg）

    198

    194

    188

    180

    （1）求出y与x之间的函数解析式；

    （2）水库前50天采用每天降低水位的办法减少捕捞成本，到达最低水位标准后，后40天水库维持最低水位进行捕捞．捕捞成本和时间的关系如下表：

    时间第x（天）

    1≤x＜50

    50≤x≤90

    捕捞成本（元/kg）

    60-x

    10

    已知鲜鱼销售单价为每千克70元，假定该养殖场每天捕捞和销售的鲜鱼没有损失，且能在当天全部售出．设销售该鲜鱼的当天收入w元（当天收入=日销售额-日捕捞成本），

    ①请写出w与x之间的函数解析式，并求出90天内哪天收入最大？当天收入是多少？

    ②若当天收入不低于4800元，请直接写出x的取值范围？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知二次函数y=ax2+bx+c（a≠0）的图象经过A（-1，0）、B（4，0）、C（0，2）三点．

    （1）求该二次函数的解析式；

    （2）点D是该二次函数图象上的一点，且满足∠DBA=∠CAO（O是坐标原点），求点D的坐标；

    （3）点P是该二次函数图象上位于一象限上的一动点，连接PA分别交BC，y轴与点E、F，若△PEB、△CEF的面积分别为S1、S2，求S1-S2的最大值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点A是y轴上一点，其坐标为（0，6），点B在x轴的正半轴上．点P，Q均在线段AB上，点P的横坐标为m，点Q的横坐标大于m，在△PQM中，若PM∥x轴，QM∥y轴，则称△PQM为点P，Q的“肩三角形．

    （1）若点B坐标为（4，0），且m＝2，则点P，B的“肩三角形”的面积为　 　；

    （2）当点P，Q的“肩三角形”是等腰三角形时，求点B的坐标；

    （3）在（2）的条件下，作过O，P，B三点的抛物线y＝ax2+bx+c

    ①若M点必为抛物线上一点，求点P，Q的“肩三角形”面积S与m之间的函数关系式，并写出自变量m的取值范围．

    ②当点P，Q的“肩三角形”面积为3，且抛物线y＝ax2+bx+c与点P，Q的“肩三角形”恰有两个交点时，直接写出m的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，Rt△ABC中，∠ABC＝90°，∠A＝30°，AC的垂直平分线交AC边于点D，交AB边于点O，以点O为圆心，OB的长为半径作圆，与AB边交于点E．

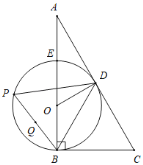
    （1）求证：AC是⊙O的切线；

    （2）若点P为⊙O上的动点（含点E，B），连接BD、BP、DP．

    ①当点P只在BE左侧半圆上时，如果BC∥DP，求∠BDP的度数；

    ②若Q是BP的中点，当BE＝4时，直接写出CQ长度的最小值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，AD是角平分钱，点E在AC上，且∠EAD=∠ADE．

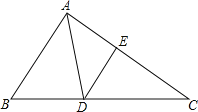
    （1）求证：△DCE∽△BCA；

    （2）若AB=3，AC=4．求DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明和小亮计划寒假结伴参加志愿者活动.小明想参加敬老服务活动，小亮想参加文明礼仪宣传活动.他们想通过做游戏来决定参加哪个活动，于是小明设计了一个游戏，游戏规则是：在一个不透明的袋子中装有编号为，，的三个球（除编号外都完全相同），从中随机摸出一个球，记下数字后放回，再从中摸出一个球，记下数字，若两次数字之和为偶数，则按照小明的想法参加敬老服务活动；若两次数字之和为奇数，则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗？请说明理由.

    查看答案和解析>>

    同步练习册答案