
【题目】水库90天内的日捕捞量y(kg)与时间第x(天)满足一次函数的关系,部分数据如表:
时间第x(天) | 1 | 3 | 6 | 10 |
日捕捞量(kg) | 198 | 194 | 188 | 180 |
(1)求出y与x之间的函数解析式;
(2)水库前50天采用每天降低水位的办法减少捕捞成本,到达最低水位标准后,后40天水库维持最低水位进行捕捞.捕捞成本和时间的关系如下表:
时间第x(天) | 1≤x<50 | 50≤x≤90 |
捕捞成本(元/kg) | 60-x | 10 |
已知鲜鱼销售单价为每千克70元,假定该养殖场每天捕捞和销售的鲜鱼没有损失,且能在当天全部售出.设销售该鲜鱼的当天收入w元(当天收入=日销售额-日捕捞成本),
①请写出w与x之间的函数解析式,并求出90天内哪天收入最大?当天收入是多少?
②若当天收入不低于4800元,请直接写出x的取值范围?
【答案】(1)y=-2x+200;(2)①第45天当天收入最大,最大收入为6050元;②当20≤x≤60时,当天收入不低于4800元
【解析】
(1)根据表格内数据,利用待定系数法即可求出y与x之间的函数解析式;
(2)①根据当天收入=日销售额-日捕捞成本即可找出w与x之间的函数解析式,再利用配方法及一次函数的性质,即可解决最值问题;
②分别求出w=-2x2+180x+2000(1≤x<50)中≥4800的x的取值范围及w=-120x+12000(50≤x≤70)中≥4800的x的取值范围,合在一起即可得出结论.
解:(1)设y与x之间的函数解析式为y=kx+b(k≠0),
将(1,198)、(3,194)代入y=kx+b中,
![]() ,解得:
,解得:![]() ,
,
∴y与x之间的函数解析式为y=-2x+200.
(2)①当1≤x<50时,w=70(-2x+200)-(-2x+200)(60-x)=-2x2+180x+2000;
当50≤x≤90时,w=70(-2x+200)-10(-2x+200)=-120x+12000.
∴w与x之间的函数解析式为w=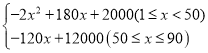 .
.
∵w=-2x2+180x+2000=-2(x-45)2+6050,
∴当x=45时,w=-2x2+180x+2000(1≤x<50)取最大值,最大值为6050;
∵w=-120x+12000中-120<0,
∴当x=50时,w=-120x+12000(50≤x≤90)取最大值,最大值为6000.
∵6050>6000,
∴第45天当天收入最大,最大收入为6050元.
②令-2x2+180x+2000≥4800,
解得:20≤x≤70,
∵20≤x<50,
∴20≤x<50;
令-120x+12000≥4800,
解得:x≤60,
∵50≤x≤70,
∴50≤x≤60.
综上所述:当20≤x≤60时,当天收入不低于4800元.


 激活思维优加课堂系列答案
激活思维优加课堂系列答案 活力试卷系列答案
活力试卷系列答案科目:初中数学 来源: 题型:
【题目】小丽和小华想利用摸球游戏决定谁去参加市里举办的书法比赛,游戏规则是:在一个不透明的袋子里装有除数字外完全相同的4个小球,上面分别标有数字2,3,4,5.一人先从袋中随机摸出一个小球,另一人再从袋中剩下的3个小球中随机摸出一个小球.若摸出的两个小球上的数字和为偶数,则小丽去参赛;否则小华去参赛.
(1)用列表法或画树状图法,求小丽参赛的概率.
(2)你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下面材料,并回答所提出的问题.
三角形内角平分线定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
已知:如图,△ABC中,AD是角平分线.
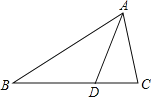
求证:![]() .
.
证明:过C作CE∥DA,交BA的延长线于E.
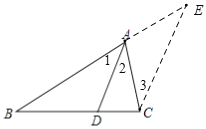
∴∠1=∠E,∠2=∠3.
∵AD是角平分线,
∴∠1=∠2.
∴∠3=∠E.
∴AC=AE.
又∵CE∥DA,
∴![]() .……①
.……①
∴![]() .
.
(1)上述证明过程中,步骤①处的理由是_____
(2)用三角形内角平分线定理解答:已知,△ABC中,AD是角平分线,AB=7cm,AC=4cm,BC=6cm,则BD的长为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2(a+1)x+a2+3=0有两个实数根x1,x2
(1)求实数a的取值范围
(2)若等腰△ABC的三边长分别为x1,x2,6,求△ABC的周长
(3)是否存在实数a,使x1,x2恰是一个边长为![]() 的菱形的两条对角线的长?若存在,求出这个菱形的面积;若不存在,说明理由.
的菱形的两条对角线的长?若存在,求出这个菱形的面积;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
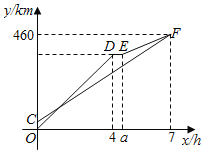
【题目】甲、乙两车从A地出发,沿同一路线驶向B地.甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地.甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60km/h;③乙出发80min追上甲;④乙刚到达货站时,甲距B地180km.其中正确是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘潭市继2017年成功创建全国文明城市之后,又准备争创全国卫生城市.某小区积极响应,决定在小区内安装垃圾分类的温馨提示牌和垃圾箱,若购买2个温馨提示牌和3个垃圾箱共需550元,且垃圾箱的单价是温馨提示牌单价的3倍.
(1)求温馨提示牌和垃圾箱的单价各是多少元?
(2)该小区至少需要安放48个垃圾箱,如果购买温馨提示牌和垃圾箱共100个,且费用不超过10000元,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,∠ACB=90°,直线l经过直角顶点C,AD⊥l,BE⊥l,垂足分别为D、E.

(1)如图,若AD=1,BE=3,求DE的长度.
(2)当直线l绕C点转动时,若AD=a,BE=b.请画出示意的图形并用含a、b的代数式直接表示出DE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com