
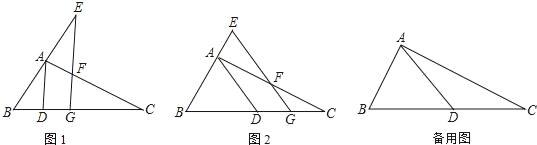
【题目】如图,Rt△ABC中,∠BAC=90°,AB=2,AC=4,D是BC边上一动点,G是BC边上的一动点,GE∥AD分别交AC、BA或其延长线于F、E两点
(1)如图1,当BC=5BD时,求证:EG⊥BC;
(2)如图2,当BD=CD时,FG+EG是否发生变化?证明你的结论;
(3)当BD=CD,FG=2EF时,DG的值= .
【答案】(1)证明见解析;(2)不变;EG+FG=2![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)利用勾股定理得出BC,进一步得出BD,之后证明△BDA∽△BAC,所以∠BDA=∠BAC=90°,根据GE∥AD进一步得出结论即可;
(2)当BD=CD时,FG+EG不发生变化,且FG+EG=![]() ,利用△CFG∽△CAD进一步证明即可得出结论;
,利用△CFG∽△CAD进一步证明即可得出结论;
(3)分两种情况:当F在CA的延长线上和E在BA的延长线上,据此分别画出图形,利用相似得出答案即可.
证明:(1)如图1,
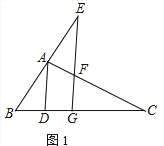
∵∠BAC=90°,AB=2,AC=4,
∴BC=2![]() ,
,
∵BC=5BD,
∴BD=![]() ,
,
∴![]() ,
,
又∵∠DBA=∠ABC,
∴△BDA∽△BAC,
∴∠BDA=∠BAC=90°,
∵EG∥AD,
∴EG⊥BC.
(2)FG=EG=2![]() 不变,
不变,
如图2,
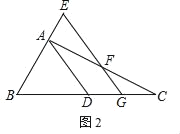
∵EG∥AD,
∴△CFG∽△CAD,
∴![]() ,
,
同理![]() ,
,
∵BD=CD,
∴![]() +
+![]() =
=![]() +
+![]() =2,
=2,
∴EG+FG=2AD,
∵BD=CD,∠BAC=90°,
∴AD=![]() BC=
BC=![]() ,
,
∴EG+FG=2AD=2![]() .
.
(3)如图,
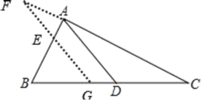
当BD=CD,FG=2EF时,
则GE=EF,
∵GE∥AD,AD∥GF,
∴△CFG∽△CAD,△ABD∽△BGE,
∴![]() ,
,![]() ,
,
∴![]() =
=![]() ,
,
又BG+CG=2![]() ,
,
∴BG=![]() ,
,
∴DG=BD=BG=![]() ;
;
如图,
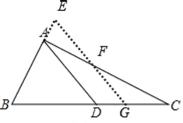
当BD=CD,FG=2EF时,
则GE=EF,
∵GE∥AD,AD∥GF,
∴△CFG∽△CAD,△ABD∽△AGE,
∴![]() ,
,![]() ,
,
∴![]() =
=![]() ,
,
又BG+CG=2![]() ,
,
∴CG=![]() ,
,
∴DG=CD﹣CG=![]() .
.
综上所知DG为![]() 或
或![]() .
.


 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案科目:初中数学 来源: 题型:
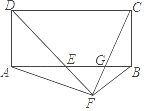
【题目】如图,在矩形ABCD中,∠ADC的平分线与AB交于E,点F在DE的延长线上,∠BFE=90°,连接AF、CF,CF与AB交于G.有以下结论:
①AE=BC
②AF=CF
③BF2=FGFC
④EGAE=BGAB
其中正确的个数是( )
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请阅读下面材料,并回答所提出的问题.
三角形内角平分线定理:三角形的内角平分线分对边所得的两条线段和这个角的两边对应成比例.
已知:如图,△ABC中,AD是角平分线.
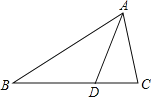
求证:![]() .
.
证明:过C作CE∥DA,交BA的延长线于E.
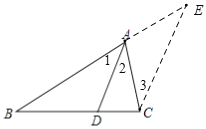
∴∠1=∠E,∠2=∠3.
∵AD是角平分线,
∴∠1=∠2.
∴∠3=∠E.
∴AC=AE.
又∵CE∥DA,
∴![]() .……①
.……①
∴![]() .
.
(1)上述证明过程中,步骤①处的理由是_____
(2)用三角形内角平分线定理解答:已知,△ABC中,AD是角平分线,AB=7cm,AC=4cm,BC=6cm,则BD的长为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
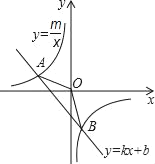
【题目】如图,已知A(4,2)、B(n,﹣4)是一次函数y=kx+b图象与反比例函数![]() 图象的两个交点.
图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)直接写出△AOB的面积;
(3)根据图象直接写出使一次函数的值小于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣2(a+1)x+a2+3=0有两个实数根x1,x2
(1)求实数a的取值范围
(2)若等腰△ABC的三边长分别为x1,x2,6,求△ABC的周长
(3)是否存在实数a,使x1,x2恰是一个边长为![]() 的菱形的两条对角线的长?若存在,求出这个菱形的面积;若不存在,说明理由.
的菱形的两条对角线的长?若存在,求出这个菱形的面积;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
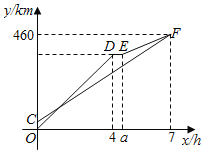
【题目】甲、乙两车从A地出发,沿同一路线驶向B地.甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地.甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60km/h;③乙出发80min追上甲;④乙刚到达货站时,甲距B地180km.其中正确是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一堂数学实践课上,赵老师给出了下列问题:
(提出问题)
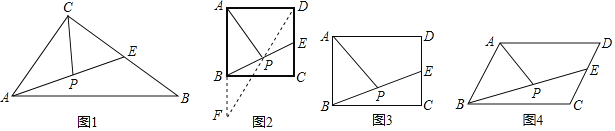
(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=90°,AC=3,AB=5.则CP= .
(探究规律)
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”,若AB=4.则AP的长为 (按图示辅助线求解);
(3)在图3中,AP是矩形ABCD的“双中线”,若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
(拓展应用)
(4)在图4中,AP是平行四边形ABCD的“双中线”,若AB=4,BC=10,∠BAD=120°.求出△ABP的周长,并说明理由?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com