
【题目】如图,已知A(4,2)、B(n,﹣4)是一次函数y=kx+b图象与反比例函数![]() 图象的两个交点.
图象的两个交点.
(1)求此反比例函数和一次函数的解析式;
(2)直接写出△AOB的面积;
(3)根据图象直接写出使一次函数的值小于反比例函数的值的x的取值范围.
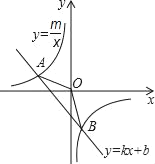
【答案】(1)y=﹣![]() ,y=﹣x﹣2;(2)S△AOB=6;(3)﹣4<x<0或x>2.
,y=﹣x﹣2;(2)S△AOB=6;(3)﹣4<x<0或x>2.
【解析】
(1)利用待定系数法即可求出函数的解析式;
(2)由(1)求出的一次函数解析式求出AB与x轴的交点坐标(-2,0),从而将△AOB分解为两个底边长为2的三角形,然后结合A、B两点纵坐标求出各自三角形面积,最后相加即可;
(3)根据一次函数的值小于反比例函数的值的x的取值范围就是对应的一次函数图像在反比例函数图像下方的自变量的取值范围求解即可.
解:(1)把(﹣4,2)代入y=![]() 得2=
得2=![]() ,则m=﹣8.
,则m=﹣8.
则反比例函数的解析式是y=﹣![]() ;
;
把(n,﹣4)代入y=﹣![]() 得n=﹣
得n=﹣![]() =2,
=2,
则B的坐标是(2,﹣4).
根据题意得:![]() ,
,![]() ,
,
解得:![]() ,
,![]() ,,
,,
∴一次函数的解析式是y=﹣x﹣2;
(2)设AB与x轴的交点是C,则C的坐标是(﹣2,0).
则OC=2,
S△AOC=2,S△BOC=4,
则S△AOB=6;
(3)由函数图象可知x的取值范围时﹣4<x<0或x>2.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() 的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
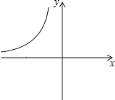
(1)图象的另一支在第________象限;在每个象限内,![]() 随
随![]() 的增大而________;
的增大而________;
(2)常数![]() 的取值范围是________;
的取值范围是________;
(3)若此反比例函数的图象经过点![]() ,求
,求![]() 的值.点
的值.点![]() 是否在这个函数图象上?点
是否在这个函数图象上?点![]() 呢?
呢?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,∠B=∠C,F为BC的中点,D,E分别为边AB,AC上的点,且∠ADF=∠AEF.
中,∠B=∠C,F为BC的中点,D,E分别为边AB,AC上的点,且∠ADF=∠AEF.
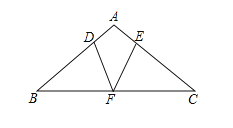
(1)求证:△BDF≌△CEF.
(2)当∠A= 100°,BD=BF时,求∠DFE的度数。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,E为AD边上的一点,过C点作CF⊥CE交AB的延长线于点F.
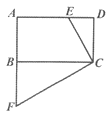
(1)求证:△CDE∽△CBF;
(2)若B为AF的中点,CB=3,DE=1,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,抛物线y=x2+ax+b经过点A(﹣2,0),B(1,3).
(1)求抛物线的解析式;
(2)由图象直接写出:x取何值时,y随x的增大而减少;
(3)根据图象回答:x取何值时,y>0.
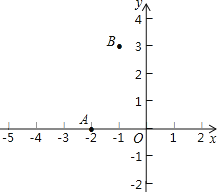
查看答案和解析>>
科目:初中数学 来源: 题型:
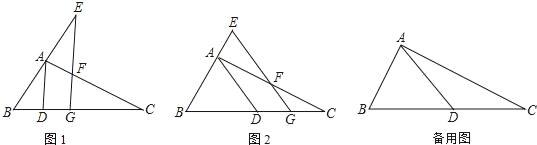
【题目】如图,Rt△ABC中,∠BAC=90°,AB=2,AC=4,D是BC边上一动点,G是BC边上的一动点,GE∥AD分别交AC、BA或其延长线于F、E两点
(1)如图1,当BC=5BD时,求证:EG⊥BC;
(2)如图2,当BD=CD时,FG+EG是否发生变化?证明你的结论;
(3)当BD=CD,FG=2EF时,DG的值= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,两个转盘中指针落在每个数字上的机会相等,现同时转动![]() 、
、![]() 两个转盘,停止后,指针各指向一个数字.小聪和小明利用这两个转盘做游戏:若两数之和为负数,则小聪胜;否则,小明胜.你认为这个游戏公平吗?如果不公平,对谁更有利?请你利用树状图或列表法说明理由.
两个转盘,停止后,指针各指向一个数字.小聪和小明利用这两个转盘做游戏:若两数之和为负数,则小聪胜;否则,小明胜.你认为这个游戏公平吗?如果不公平,对谁更有利?请你利用树状图或列表法说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的图象经过A(-1,0)、B(4,0)、C(0,2)三点.
(1)求该二次函数的解析式;
(2)点D是该二次函数图象上的一点,且满足∠DBA=∠CAO(O是坐标原点),求点D的坐标;
(3)点P是该二次函数图象上位于一象限上的一动点,连接PA分别交BC,y轴与点E、F,若△PEB、△CEF的面积分别为S1、S2,求S1-S2的最大值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,现给出以下四个结论:(1)AE=CF;(2)△EPF是等腰直角三角形;(3)S四边形AEPF=![]() S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )
S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )

A.1个B.3个C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com