
【题目】在一堂数学实践课上,赵老师给出了下列问题:
(提出问题)
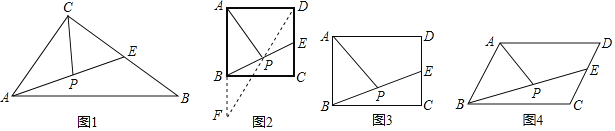
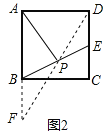
(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=90°,AC=3,AB=5.则CP= .
(探究规律)
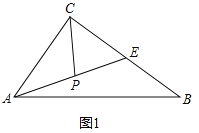
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”,若AB=4.则AP的长为 (按图示辅助线求解);
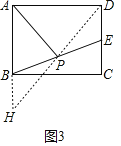
(3)在图3中,AP是矩形ABCD的“双中线”,若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
(拓展应用)
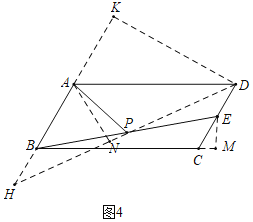
(4)在图4中,AP是平行四边形ABCD的“双中线”,若AB=4,BC=10,∠BAD=120°.求出△ABP的周长,并说明理由?
【答案】(1)![]() ;(2)
;(2)![]() ;(3)3
;(3)3![]() ;(4)△ABP的周长为4+
;(4)△ABP的周长为4+![]() .
.
【解析】
(1)利用勾股定理求出AE,再利用直角三角形斜边中线的性质即可解决问题.
(2)利用勾股定理求出DF,再利用直角三角形斜边中线的性质即可解决问题.
(3)如图3中,连接DP,延长DP交AB的延长线于H.利用全等三角形的性质以及勾股定理求出DH即可解决问题.
(4)如图4中,连接DP,延长DP交AB的延长线于H,作DK⊥BA交BA的延长线于K,AN⊥DH于N,EM⊥BC交BC的延长线于M.分别求出BP,AP即可解决问题.
解:(1)如图1中,
在Rt△ABC中,∵∠ACB=90°,AB=5,AC=3,
∴BC=![]()
∵E是BC的中点,
∴EC=EB=2,
∴AE=![]()
∵P是AE的中点,
∴PC=![]() AE=
AE=![]() .
.
故答案为![]() .
.
(2)如图2中,连接DP,延长DP交AB的延长线于F.
∵四边形ABCD是正方形,
∴AB=CD=4,AB∥CD,∠FAD=90°,
∴∠F=∠PDE,
∵PB=PE,∠FPB=∠EPD,
∴△FPB≌△DPE(AAS),
∴DP=PF,BF=DE=![]() CD=2,AF=AB+B4=2=6,
CD=2,AF=AB+B4=2=6,
在Rt△ADF中,DF=![]()
∵DP=PF,
∴AP=![]() DF=
DF=![]() ,
,
故答案为![]() .
.
(3)如图3中,连接DP,延长DP交AB的延长线于H.
同法可证:∠DAB=90°,△HPB≌△DPE,
∴DE=BH=![]() CD=2,DP=PH,AHAB+BH=6,
CD=2,DP=PH,AHAB+BH=6,
在Rt△ADH中,DH=![]()
∵DP=PH,
∴PA=![]() DH=
DH=![]() .
.
(4)如图4中,连接DP,延长DP交AB的延长线于H,作DK⊥BA交BA的延长线于K,AN⊥DH于N,EM⊥BC交BC的延长线于M.
∵四边形ABCD是平行四边形,
∴∠BAD=∠BCD=120°,AB=CD=4,AD=BC=10,
在Rt△ADK中,∵∠KAD=60°,∠K=90°,AD=10,
∴AK=![]() AD=5,KD=
AD=5,KD=![]() AK=
AK=![]() ,
,
在Rt△ECM中,∵∠M=90°,∠ECM=60°,EC=![]() CD=2,
CD=2,
∴CM=![]() EC=1,EM=
EC=1,EM=![]() ,
,
在Rt△BEM中,BE=![]()
∵P是BE的中点,
∴PB=![]() EB=
EB=![]() ,
,
∵△PBH≌△PED,
∴DP=PH,DE=BH=2,HK=BH+AB+AK=2+4+5=11,
∴DH=![]()
∴PH=PD=7,
∵∠AHN=∠DHE,∠ANH=∠K=90°,
∴△HAN∽△HDK,
∴![]()
∴![]()
∴AN=![]() ,HN=
,HN=![]() ,
,
∴PN=PH﹣HN=7﹣![]() =
=![]() ,
,
∵AN⊥DH,
∴PA=![]()
∴△ABP的周长=AB+PA+PB=![]()


科目:初中数学 来源: 题型:
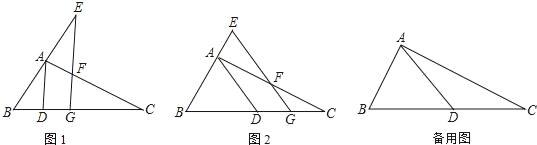
【题目】如图,Rt△ABC中,∠BAC=90°,AB=2,AC=4,D是BC边上一动点,G是BC边上的一动点,GE∥AD分别交AC、BA或其延长线于F、E两点
(1)如图1,当BC=5BD时,求证:EG⊥BC;
(2)如图2,当BD=CD时,FG+EG是否发生变化?证明你的结论;
(3)当BD=CD,FG=2EF时,DG的值= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,∠A=30°,AC的垂直平分线交AC边于点D,交AB边于点O,以点O为圆心,OB的长为半径作圆,与AB边交于点E.
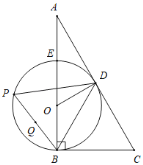
(1)求证:AC是⊙O的切线;
(2)若点P为⊙O上的动点(含点E,B),连接BD、BP、DP.
①当点P只在BE左侧半圆上时,如果BC∥DP,求∠BDP的度数;
②若Q是BP的中点,当BE=4时,直接写出CQ长度的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD是角平分钱,点E在AC上,且∠EAD=∠ADE.
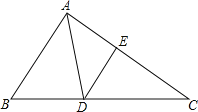
(1)求证:△DCE∽△BCA;
(2)若AB=3,AC=4.求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,∠BAC=90°,直角∠EPF的顶点P是BC的中点,两边PE,PF分别交AB,AC于点E,F,现给出以下四个结论:(1)AE=CF;(2)△EPF是等腰直角三角形;(3)S四边形AEPF=![]() S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )
S△ABC;(4)当∠EPF在△ABC内绕顶点P旋转时始终有EF=AP.(点E不与A、B重合),上述结论中是正确的结论的概率是( )

A.1个B.3个C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
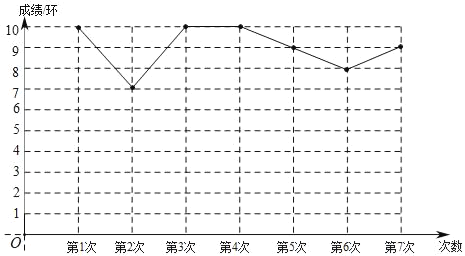
【题目】嘉淇同学利用业余时间进行射击训练,一共射击7次,经过统计,制成如图12所示的折线统计图.
(1)这组成绩的众数是 ;
(2)求这组成绩的方差;
(3)若嘉淇再射击一次(成绩为整数环),得到这8次射击成绩的中位数恰好就是原来7次成绩的中位数,求第8次的射击成绩的最大环数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为6的⊙O中,正六边形ABCDEF与正方形AGDH都内接于⊙O,则图中阴影部分的面积为( )

A. 27﹣9![]() B. 18
B. 18![]() C. 54﹣18
C. 54﹣18![]() D. 54
D. 54
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小亮计划寒假结伴参加志愿者活动.小明想参加敬老服务活动,小亮想参加文明礼仪宣传活动.他们想通过做游戏来决定参加哪个活动,于是小明设计了一个游戏,游戏规则是:在一个不透明的袋子中装有编号为![]() ,
,![]() ,
,![]() 的三个球(除编号外都完全相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和为偶数,则按照小明的想法参加敬老服务活动;若两次数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.
的三个球(除编号外都完全相同),从中随机摸出一个球,记下数字后放回,再从中摸出一个球,记下数字,若两次数字之和为偶数,则按照小明的想法参加敬老服务活动;若两次数字之和为奇数,则按照小亮的想法参加文明礼仪宣传活动.你认为这个游戏公平吗?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O中的弦BC等于⊙O的半径,延长BC到D,使BC=CD,点A为优弧BC上的一个动点,连接AD,AB,AC,过点D作DE⊥AB,交直线AB于点E,当点A在优弧BC上从点C运动到点B时,则DE+AC的值的变化情况是( )
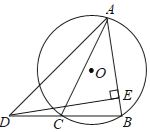
A.不变B.先变大再变小C.先变小再变大D.无法确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com