
【题目】如图,在半径为6的⊙O中,正六边形ABCDEF与正方形AGDH都内接于⊙O,则图中阴影部分的面积为( )

A. 27﹣9![]() B. 18
B. 18![]() C. 54﹣18
C. 54﹣18![]() D. 54
D. 54
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车从A地出发,沿同一路线驶向B地.甲车先出发匀速驶向B地,40min后,乙车出发,匀速行驶一段时间后,在途中的货站装货耗时半小时.由于满载货物,为了行驶安全,速度减少了50km/h,结果与甲车同时到达B地.甲乙两车距A地的路程y(km)与乙车行驶时间x(h)之间的函数图象如图所示,则下列说法:①a=4.5;②甲的速度是60km/h;③乙出发80min追上甲;④乙刚到达货站时,甲距B地180km.其中正确是( )
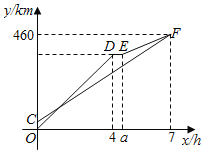
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,人工喷泉有一个竖直的喷水枪AB,喷水口A距地面2.25m,喷出水流的运动路线是抛物线.水流的最高点P到喷水枪AB所在直线的距离为1m,且到地面的距离为3m.求水流的落地点C到水枪底部B的距离.
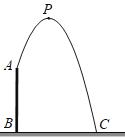
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一堂数学实践课上,赵老师给出了下列问题:
(提出问题)
(1)如图1,在△ABC中,E是BC的中点,P是AE的中点,就称CP是△ABC的“双中线”,∠ACB=90°,AC=3,AB=5.则CP= .
(探究规律)
(2)在图2中,E是正方形ABCD一边上的中点,P是BE上的中点,则称AP是正方形ABCD的“双中线”,若AB=4.则AP的长为 (按图示辅助线求解);
(3)在图3中,AP是矩形ABCD的“双中线”,若AB=4,BC=6,请仿照(2)中的方法求出AP的长,并说明理由;
(拓展应用)
(4)在图4中,AP是平行四边形ABCD的“双中线”,若AB=4,BC=10,∠BAD=120°.求出△ABP的周长,并说明理由?
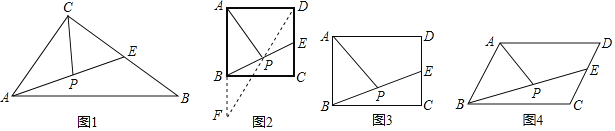
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+(2k+1)x+k2+1=0.
(1)当方程有一个根为﹣1时,求k的值及另一个根;
(2)当方程有两个不相等的实数根,求k的取值范围;
(3)若方程两实根x1、x2满足x1+x2=x1x2,求k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AC=BC,∠ACB=90°,直线l经过直角顶点C,AD⊥l,BE⊥l,垂足分别为D、E.

(1)如图,若AD=1,BE=3,求DE的长度.
(2)当直线l绕C点转动时,若AD=a,BE=b.请画出示意的图形并用含a、b的代数式直接表示出DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】哈尔滨市滑雪业提前进入旺季,某体育用品商店购进一批简易滑雪板,每件进价为100元,售价为130元,每星期可卖出80件.商家决定降价促销,根据市场调查,每降价5元,每星期可多卖出20件.
(1)设商家每件售价x元,每星期的销售数量为y元,求y与x之间的函数关系式;
(2)降价后,商家要使每星期的销售利润W最大,应将售价定为多少元?最大销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等边△ABC中,以BC为弦的⊙O分别与AB,AC交于点D和E,点F是BC延长线上一点,CF=AE,连接EF.
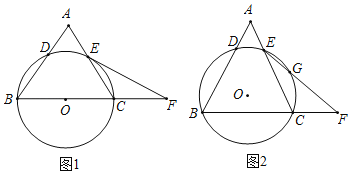
(1)如图1,BC为直径,求证:EF是⊙O的切线;
(2)如图2,EF与⊙O交于点G,⊙O的半径为1,BC的长为![]() π,求BF的长.
π,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们县是紫菜生产大县,某景点商户向游客推销一种加工好的优质紫菜,已知每千克成本为20元.市场调查发现,在一段时间内,该产品销售量![]() (千克)与销售单价
(千克)与销售单价![]() (元/千克)的变化而变化有如下关系式:
(元/千克)的变化而变化有如下关系式:![]() .设这种紫菜在这段时间内的销售利润为
.设这种紫菜在这段时间内的销售利润为![]() (元).
(元).
(1)求![]() 与
与![]() 的关系式;
的关系式;
(2)当销售价定为多少元时,每天的销售利润最大?最大利润是多少?
(3)如果物价部门规定该景区这种紫菜的销售单价不得高于28元/千克,该商户每天能否获得比150元更大的利润?如果能请求出最大利润,如果不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com