
【题目】[发现]如图∠ACB=∠ADB=90°,那么点D在经过A,B,C三点的圆上(如图①)

[思考]如图②,如果∠ACB=∠ADB=a(a≠90°)(点C,D在AB的同侧),那么点D还在经过A, B,C三点的圆上吗?
我们知道,如果点D不在经过A,B,C三点的圆上,那么点D要么在圆O外,要么在圆O内,以下该同学的想法说明了点D不在圆O外。
请结合图④证明点D也不在⊙O内.

[结论]综上可得结论:如图②,如果∠ACB=∠ADB=a(点C,D在AB的同侧),那么点D在经过A,B,C三点的圆上,即:点A、B、C、D四点共圆。
[应用]利用上述结论解决问题:
如图⑤,已知△ABC中,∠C=90°,将△ACB绕点A顺时针旋转一个角度得△ADE,连接BE CD,延长CD交BE于点F,
(1)求证:点B、C、A、F四点共圆;
(2)求证:BF=EF.

图⑤
【答案】【思考】证明见解析;【应用】(1证明见解析;(2)证明见解析
【解析】试题分析:【思考】假设点D在⊙O内,利用圆周角定理及三角形外角的性质,可证得与条件相矛盾的结论,从而证得点D不在⊙O内;
[应用]
(1)由旋转的性质可得∠ACD=∠ABE,故B、C、A、F四点共圆,
(2)由圆内接四边形的性质得∠BCA+∠BFA=180°即可证明.
【思考】
【证】如图,假设点D在⊙O内,延长AD交⊙O于点E,连接BE;则∠AEB=∠ACB

∵∠ADB是△DBE的一个外角
∴∠ADB>∠AEB
∴∠ADB>∠ACB
这与条件∠ACB=∠ADB矛盾
∴点D不在⊙O内
【应用】【证】(1)∵AC=AD,AB=AE,
∴∠ACD=∠ADC,∠ABE=∠AEB,
∵∠CAB=∠DAE,
∴∠CAD=∠BAE,
∵2∠ACD+∠CAD=180°,2∠ABE+∠BAE=180°,
∴∠ACD=∠ABE,
∴B、C、A、F四点共圆,
(2)∵B、C、A、F四点共圆,
∴∠BFA+∠BCA=180°,
∵∠ACB=90°,∴∠BFA=90°,
∴AF⊥BE,
∵AB=AE,
∴BF=EF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,线段AB,C是线段AB上一点,M是AB的中点,N是AC的中点. ![]()
(1)若AB=8cm,AC=3.2cm,求线段MN的长;
(2)若BC=a,试用含a的式子表示线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)等腰三角形一腰上的中线将这个等腰三角形的周长分成15 cm和6 cm两部分.求等腰三角形的底边长.

(2)已知等腰三角形中,有一个角比另一个角的2倍少20°,求顶角的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义探究题 如果ac=b,那么我们规定(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,计算:(3,27),(4,16);
(2)记(3,5)=a,(3,6)=b,(3,30)=c,试说明:a+b=c.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店的老板销售服装,他要以不低于进价120%的价格才能出售,但为了获得更多利润,他以高出进价80%的价格标价,若你想买下标价为360元的大衣,最多降价____元.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如果AF=4,AB=7. 
(1)求BE的长;
(2)在图中作出延长BE与DF的交点G,并说明BG⊥DF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了推动运动普及,拟成立多个球类运动社团,为此,学生会采取抽样调查的方法,从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好(要求每位同学只能选择其中一种自己喜欢的球类运动),并将调查结果绘制成了如下条形统计图和扇形统计图(不完整).请你根据图中提供的信息,解答下列问题: 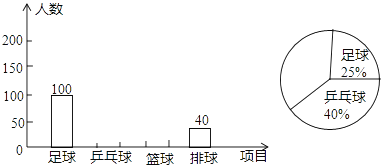
(1)本次调查的学生共有多少人;
(2)请将条形统计图和扇形统计图补充完整;
(3)若该学校共有学生2000人,根据以上数据分析,试估计选择足球运动的同学有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形纸片ABCD中,![]() ,将纸片折叠,点A、D分别落在A′、D′处,且A′D′经过B,EF为折痕,当D′F
,将纸片折叠,点A、D分别落在A′、D′处,且A′D′经过B,EF为折痕,当D′F![]() CD时,
CD时,![]() 的值为__________.
的值为__________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com