
����Ŀ��ijѧУΪ���ƶ��˶��ռ����������������˶����ţ�Ϊ�ˣ�ѧ�����ȡ��������ķ�����������ƹ�������������ĸ���Ŀ������������ѧ������Ȥ���ã�Ҫ��ÿλͬѧֻ��ѡ������һ���Լ�ϲ���������˶������������������Ƴ�����������ͳ��ͼ������ͳ��ͼ�������������������ͼ���ṩ����Ϣ������������⣺ 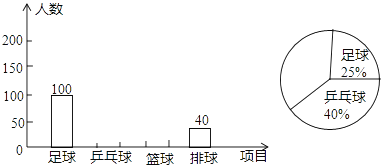
��1�����ε����ѧ�����ж����ˣ�
��2���뽫����ͳ��ͼ������ͳ��ͼ����������
��3������ѧУ����ѧ��2000�ˣ������������ݷ������Թ���ѡ�������˶���ͬѧ�ж����ˣ�
���𰸡�
��1���⣺100��25%=400���ˣ���
�ʱ��ε����ѧ������400��
��2���⣺ϲ��ƹ�����������400��40%=160���ˣ���ϲ�������������400��100��160��40=100���ˣ���
������ռ�İٷֱ�Ϊ�� ![]() ��100%=25%��������ռ�İٷֱ�Ϊ��
��100%=25%��������ռ�İٷֱ�Ϊ�� ![]() ��100%=10%��
��100%=10%��
��ͼ��ʾ��
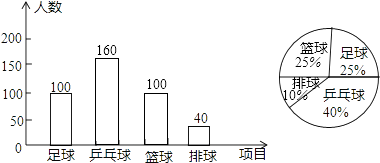
��3���⣺ѡ�������˶���ѧ������Ϊ��2000��25%=500���ˣ���
�ʹ���ѡ�������˶���ͬѧ��500��
����������1������ϲ���������������ռ�İٷֱ���ʽ���㼴����������ѧ������������2���ֱ�����ϲ��ƹ����������������Լ�����������ռ�İٷֱȣ����ɲ�ȫͳ��ͼ����3����ѧ������2000����ѡ�������˶���ռ�İٷֱȣ����ɽ��
�����㾫��������ȫ�������������������ͳ��ͼ����Ŀ�����жϼ��ɵõ��𰸣���Ҫ��֪ȫ������ռ���������ȫ�桢ȷ����һ�㻨�Ѷࡢ��ʱ��������ijЩ���鲻����ȫ����飻����������л����١�ʡʱ���ص㣬����ȡ�������Ƿ���д����ԣ�ֱ�ӹ�ϵ����������Ƶ�ȷ�̶ȣ�������ر�ʾ������������������ռ�İٷֱȣ����Dz�������ر�ʾ��ÿ����Ŀ�ľ�����Ŀ�Լ�����ı仯�����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
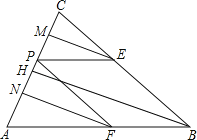
����Ŀ����ͼ����ABC�У�AB=BC��AC=8��tanA=k��PΪAC����һ���㣬��PC=x����PE��AB��BC��E��PF��BC��AB��F��
��1��֤������PCE�ǵ��������Σ�
��2��EM��FN��BH�ֱ�����PEC����AFP����ABC�ĸߣ��ú�x��k�Ĵ���ʽ��ʾEM��FN����̽��EM��FN��BH֮���������ϵ��
��3����k=4ʱ�����ı���PEBF�����S��x�ĺ�����ϵʽ��xΪ��ֵʱ��S�����ֵ�������S�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��[����]��ͼ��ACB=��ADB=90�㣬��ô��D�ھ���A��B��C�����Բ�ϣ���ͼ����

[˼��]��ͼ���������ACB=��ADB=a��a��90�㣩����C��D��AB��ͬ�ࣩ����ô��D���ھ���A�� B��C�����Բ����
����֪���������D���ھ���A��B��C�����Բ�ϣ���ô��DҪô��ԲO�⣬Ҫô��ԲO�ڣ����¸�ͬѧ���뷨˵���˵�D����ԲO�⡣
����ͼ��֤����DҲ������O��.

[����]���Ͽɵý��ۣ���ͼ���������ACB=��ADB=a����C��D��AB��ͬ�ࣩ����ô��D�ھ���A��B��C�����Բ�ϣ�������A��B��C��D�ĵ㹲Բ��
[Ӧ��]�����������۽�����⣺
��ͼ������֪��ABC�У���C=90�㣬����ACB�Ƶ�A˳ʱ����תһ���Ƕȵ���ADE������BE CD���ӳ�CD��BE�ڵ�F��
��1����֤����B��C��A��F�ĵ㹲Բ��
��2����֤��BF=EF.

ͼ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������m2+n2+2m-6n+10=0���ǣ�������
A. m=1��n=3 B. m=1��n=-3 C. m=-1��n=-3 D. m=-1��n=3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����OAC����BAD���ǵ���ֱ�������Σ���ACO=��ADB=90�㣬����������![]() �ڵ�һ����ͼ����B������OAC����BAD�����֮��S��OAC��S��BADΪ�� ��
�ڵ�һ����ͼ����B������OAC����BAD�����֮��S��OAC��S��BADΪ�� ��

A. 36 B. 12 C. 6 D. 3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��1�·ݲ���Ϊa�֣��Ժ�ÿ���±���һ��������x%����ó�3�·ݵIJ�������λ���֣�Ϊ��������
A.a��1+x��2
B.a��1+x%��2
C.a+ax%
D.a+a��x%��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������a+b��2����a��b��2��4����һ���������ǣ�������
A. a��b���෴��B. a�ǩ�b���෴��
C. a��b�ĵ���D. a�ǩ�b�ĵ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����м�����ȷ���ǣ�������
A. 2a2+3a2��5a4B. 3a��2a��1C. 2a2��a3��2a6D. ��a2��3��a6
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ڶ��κ���y=��x-1��2+2��ͼ������˵����ȷ���ǣ� ��
A. �������� B. ��x=-1,ʱ��y�����ֵ��2 C. �Գ�����x=-1 D. ���������ǣ�1,2��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com