
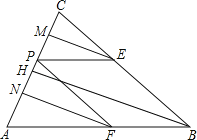
【题目】如图,△ABC中,AB=BC,AC=8,tanA=k,P为AC边上一动点,设PC=x,作PE∥AB交BC于E,PF∥BC交AB于F.
(1)证明:△PCE是等腰三角形;
(2)EM、FN、BH分别是△PEC、△AFP、△ABC的高,用含x和k的代数式表示EM、FN,并探究EM、FN、BH之间的数量关系;
(3)当k=4时,求四边形PEBF的面积S与x的函数关系式.x为何值时,S有最大值?并求出S的最大值.
【答案】解:(1)证明:∵AB=BC,∴∠A=∠C。
∵PE∥AB,∴∠CPE=∠A。
∴∠CPE=∠C。∴△PCE是等腰三角形。
(2)∵△PCE是等腰三角形,EM⊥CP,∴CM=![]() CP=
CP=![]() ,tanC=tanA=k。
,tanC=tanA=k。
∴EM=CMtanC=![]() k=
k=![]() 。
。
同理:FN=ANtanA=![]() k=4k﹣
k=4k﹣![]() 。
。
由于BH=AHtanA=![]() ×8k=4k,EM+FN=
×8k=4k,EM+FN=![]() +4k﹣
+4k﹣![]() =4k,
=4k,
∴EM+FN=BH。
(3)当k=4时,EM=2x,FN=16﹣2x,BH=16,
∴S△PCE=![]() x2x=x2,S△APF=
x2x=x2,S△APF=![]() (8﹣x)(16﹣2x)=(8﹣x)2,S△ABC=
(8﹣x)(16﹣2x)=(8﹣x)2,S△ABC=![]() ×8×16=64。
×8×16=64。
∴![]() 。
。
∴当k=4时,四边形PEBF的面积S与x的函数关系式为![]() 。
。
∵![]() ,
,
∴当x=4时,S有最大值32。
【解析】(1)根据等边对等角可得∠A=∠C,然后根据两直线平行,同位角相等求出∠CPE=∠A,从而得到∠CPE=∠C,即可得证。
(2)根据等腰三角形三线合一的性质求出CM=![]() CP,然后求出EM,同理求出FN、BH的长,再根据结果整理可得EM+FN=BH。
CP,然后求出EM,同理求出FN、BH的长,再根据结果整理可得EM+FN=BH。
(3)分别求出EM、FN、BH,然后根据S△PCE,S△APF,S△ABC,再根据![]() ,整理即可得到S与x的关系式,然后利用二次函数的最值问题解答。
,整理即可得到S与x的关系式,然后利用二次函数的最值问题解答。


 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:初中数学 来源: 题型:
【题目】如图,线段AB,C是线段AB上一点,M是AB的中点,N是AC的中点. ![]()
(1)若AB=8cm,AC=3.2cm,求线段MN的长;
(2)若BC=a,试用含a的式子表示线段MN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解长城小区“全民健身”活动的开展情况,随机对该小区的40名居民一周的体育锻炼时间进行了统计,结果如表:
锻炼时间(时) | 3 | 4 | 5 | 6 | 7 |
人数(人) | 6 | 13 | 14 | 5 | 2 |
这40名居民一周体育锻炼时间的中位数是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班的中考英语听力口语模拟考试成绩如下:
考试成绩/分 | 30 | 29 | 28 | 27 | 26 |
学生数/人 | 20 | 15 | 10 | 2 | 2 |
该班中考英语听力口语模拟考试成绩的众数比中位数多______分.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)等腰三角形一腰上的中线将这个等腰三角形的周长分成15 cm和6 cm两部分.求等腰三角形的底边长.

(2)已知等腰三角形中,有一个角比另一个角的2倍少20°,求顶角的度数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】新定义探究题 如果ac=b,那么我们规定(a,b)=c.例如:因为23=8,所以(2,8)=3.
(1)根据上述规定,计算:(3,27),(4,16);
(2)记(3,5)=a,(3,6)=b,(3,30)=c,试说明:a+b=c.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了推动运动普及,拟成立多个球类运动社团,为此,学生会采取抽样调查的方法,从足球、乒乓球、篮球、排球四个项目调查了若干名学生的兴趣爱好(要求每位同学只能选择其中一种自己喜欢的球类运动),并将调查结果绘制成了如下条形统计图和扇形统计图(不完整).请你根据图中提供的信息,解答下列问题: 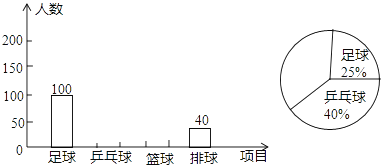
(1)本次调查的学生共有多少人;
(2)请将条形统计图和扇形统计图补充完整;
(3)若该学校共有学生2000人,根据以上数据分析,试估计选择足球运动的同学有多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com