
【题目】如图,直线AB过点A(3,0),B(0,2)
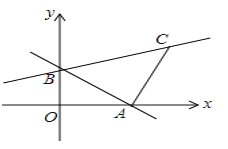
(1)求直线AB的解析式。
(2)过点A作AC⊥AB且AC∶AB=3∶4,求过B、C两点直线的解析式.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)用待定系数法直接代入A,B的坐标即可;
(2)过C点作CD⊥x轴于D点,用三角形的相似求出C点的坐标,再用待定系数法求过B、C两点直线的解析式即可.
(1)设直线AB的解析式为:![]()
代入A(3,0),B(0,2)得:
![]()
解得: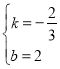
∴直线AB的解析式为![]()
(2)如图:过C点作CD⊥x轴于D点,
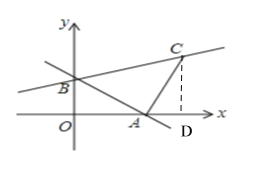
∵AC⊥AB
∴∠CAD+∠OAB=90°,∠OAB+∠OBA=90°
∴∠CAD=∠OBA
又∠BOA=∠ADC=90°
∴△AOB∽CDA
∴![]()
∵AC∶AB=3∶4
∴![]()
∴![]()
所以C点的坐标为![]()
设直线BC的解析式为:![]()
代入B(0,2),C ![]() 得:
得:
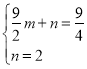
解得: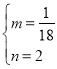
∴过B、C两点直线的解析式为:![]()


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
【题目】(1)已知某抛物线与抛物线y=﹣2x2+3x﹣1的形状和开口方向都相同,并且其对称轴为x=1,函数的最大值为4,求此抛物线的解析式;
(2)已知一个二次函数图象经过(﹣1,10),(1,4),(2,7)三点,求它的解析式;
(3)某抛物线过点(1,0),(﹣2,0)并且与直线y=2x﹣1的交点的纵坐标为5,求此抛物线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论:①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若![]() ,则3S△EDH=13S△DHC,其中结论正确的序号有__.
,则3S△EDH=13S△DHC,其中结论正确的序号有__.
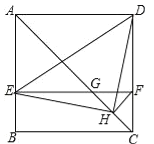
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,DE是⊙O的直径,AB是⊙O的弦,AB的中点C在直径DE上.已知AB=8cm,CD=2cm
(1)求⊙O的面积;
(2)连接AE,过圆心O向AE作垂线,垂足为F,求OF的长.
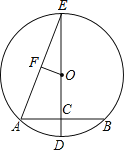
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解方程。
(1)4(x-3) ![]() =36
=36
(2)x2-4x+1=0.
(3)![]() -7x+6=0
-7x+6=0
(4)![]()
(5)(y-1)2+2y(1-y)=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是一次函数y=2x的图象与反比例函数y=![]() 的图象在第一象限内的交点,AB⊥x轴于点B,点C在x轴的负半轴上,且∠ACB=∠OAB,△OAB的面积为4,则点C的坐标为( )
的图象在第一象限内的交点,AB⊥x轴于点B,点C在x轴的负半轴上,且∠ACB=∠OAB,△OAB的面积为4,则点C的坐标为( )

A.(﹣8,0)B.(﹣6,0)C.(﹣![]() ,0)D.(﹣
,0)D.(﹣![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象与反比例函数![]() 的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
求:(1)一次函数的解析式;
(2)△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com