【题目】如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．
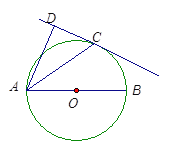
（1）求证：AD⊥DC；
（2）若AD＝2，AC＝
，求AB的长．
【答案】（1）略 （2）2.5
【解析】
（1）连接OC，根据切线的性质得到OC与CD垂直，进而得到∠OCA+∠DCA=90°，由AC为角平分线，根据角平分线定义得到两个角相等，又OA=OC，根据等边对等角得到又得到另两个角相等，等量代换后得到∠DAC=∠OCA，根据等角的余角相等得到∠DCA+∠DAC=90°，从而得到∠ADC为直角，得证；
（2）连接CB，由AB为圆O的直径，根据直径所对的圆周角为直角得到∠ACB与∠ADC相等都为直角，又根据AC为角平分线得到一对角相等，由两对对应角相等的两三角形相似，得到三角形ADC与三角形ABC相似，由相似得比例列出关系式，把AC和AD的长即可求出AB的长．
科目：初中数学 来源： 题型：
【题目】如图，二次函数y=ax2+bx+c（a≠0）的图象的顶点在第一象限，且过点（0，1）和（﹣1，0），下列结论：①ab＜0，②b2＞4，③0＜a+b+c＜2，④0＜b＜1，⑤当x＞﹣1时，y＞0．其中正确结论的个数是（ ）
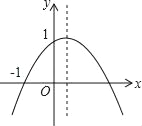
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】阅读资料：阅读材料，完成任务：材料 阿尔·花拉子密(约 780～约 850)，著名数学家、天文学家、地理学家，是代数与算术的整理者，被誉为“代数之父”。
他用以下方法求得一元二次方程 x2＋2x－35＝0 的解：
将边长为 x 的正方形和边长为 1 的正方形，外加两个长方形，长为 x，宽为 1，拼合在一起的面积是 x2＋2×x×1＋1×1，而由 x2＋2x－35＝0 变形得 x2＋2x＋1＝35＋1（如图所示），即右边边长为 x＋1 的正方形面积为 36。
所以(x＋1)2＝36，则 x＝5.
任务：请回答下列问题
(1)上述求解过程中所用的方法是( )
A.直接开平方法 B．公式法 C．配方法 D．因式分解法
(2)所用的数学思想方法是( ) 的的
A.分类讨论思想 B.数形结合思想 C.转化思想 D.公理化思想
(3)运用上述方法构造出符合方程 x2＋8x－9＝0 的一个正根的正方形
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在□ABCD中，经过A、B、C三点的⊙O与AD相切于点A，经过点C的切线与AD的延长线相交于点P，连接AC．
（1）求证：AB＝AC；
（2）若AB＝4，⊙O的半径为
，求PD的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】初三一班五个劳动竞赛小组一天植树的棵数是：10，10，12，x，8，如果这组数据的众数与平均数相等，那么这组数据的中位数是（ ）
A. 12 B. 10 C. 9 D. 8
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在直角坐标系中，△OBA和△DOC的边OA、OC都在x轴的正半轴上，点B的坐标为（6，8），∠BAO
∠OCD90°，OD5，CD3．反比例函数
的图象经过点D，交AB边于点E．
（1）求k的值；（2）求BE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，直线AB过点A（3,0），B（0,2）
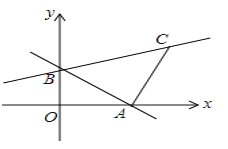
（1）求直线AB的解析式。
（2）过点A作AC⊥AB且AC∶AB=3∶4，求过B、C两点直线的解析式．
查看答案和解析>>
科目：初中数学 来源： 题型：
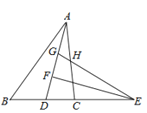
【题目】如图，在
中，4AB=5AC，AD为的角平分线，点E在BC的延长线上，
于点F，点G在AF上，FG=FD，连接EG交AC于点H，若点H是AC的中点，则
的值为___________
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
