
【题目】如图,在![]() 中,4AB=5AC,AD为
中,4AB=5AC,AD为![]() 的角平分线,点E在BC的延长线上,
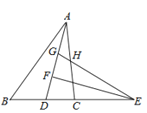
的角平分线,点E在BC的延长线上,![]() 于点F,点G在AF上,FG=FD,连接EG交AC于点H,若点H是AC的中点,则
于点F,点G在AF上,FG=FD,连接EG交AC于点H,若点H是AC的中点,则![]() 的值为___________
的值为___________
【答案】![]()
【解析】
利用角平分线的性质,得到BD=![]() CD;延长AC,构造一对全等三角形△ABD≌△AMD;
CD;延长AC,构造一对全等三角形△ABD≌△AMD;
过点M作MN∥AD,由MD=BD=KD=![]() CD,得到等腰△DMK;然后利用角之间关系证明DM∥GN,从而推出四边形DMNG为平行四边形;由MN∥AD,列出比例式,求出
CD,得到等腰△DMK;然后利用角之间关系证明DM∥GN,从而推出四边形DMNG为平行四边形;由MN∥AD,列出比例式,求出![]() 的值.
的值.
解:已知AD为角平分线,则点D到AB、AC的距离相等,设为h.
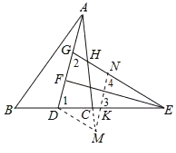
∵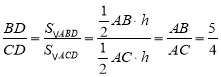 ,
,
∴BD=![]() CD.
CD.
如图,延长AC,在AC的延长线上截取AM=AB,则有AC=4CM.连接DM.
在△ABD与△AMD中,AB=AM,∠BAD=∠MAD,AD=AD,
∴△ABD≌△AMD(SAS),
∴MD=BD=![]() CD.
CD.
过点M作MN∥AD,交EG于点N,交DE于点K.
∵MN∥AD,
∴![]() ,
,
∴CK=![]() CD,
CD,
∴KD=![]() CD.
CD.
∴MD=KD,即△DMK为等腰三角形,
∴∠DMK=∠DKM.
由题意,易知△EDG为等腰三角形,且∠1=∠2;
∵MN∥AD,
∴∠3=∠4=∠1=∠2,
又∵∠DKM=∠1,
∴∠DMK=∠4,
∴DM∥GN,
∴四边形DMNG为平行四边形,
∴MN=DG=2FD.
∵点H为AC中点,AC=4CM,
∴![]() .
.
∵MN∥AD,
∴![]() ,即
,即![]() ,
,
∴![]() .
.
故答案为:![]() .
.


 快捷英语周周练系列答案
快捷英语周周练系列答案科目:初中数学 来源: 题型:
【题目】用适当的方法解方程。
(1)4(x-3) ![]() =36
=36
(2)x2-4x+1=0.
(3)![]() -7x+6=0
-7x+6=0
(4)![]()
(5)(y-1)2+2y(1-y)=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知点A是一次函数y=2x的图象与反比例函数y=![]() 的图象在第一象限内的交点,AB⊥x轴于点B,点C在x轴的负半轴上,且∠ACB=∠OAB,△OAB的面积为4,则点C的坐标为( )
的图象在第一象限内的交点,AB⊥x轴于点B,点C在x轴的负半轴上,且∠ACB=∠OAB,△OAB的面积为4,则点C的坐标为( )

A.(﹣8,0)B.(﹣6,0)C.(﹣![]() ,0)D.(﹣
,0)D.(﹣![]() ,0)
,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长度为5的动线段AB分别与坐标系横轴、纵轴的正半轴交于点A、点B,点O和点C关于AB对称,连接CA、CB,过点C作x轴的垂线段CD,交x轴于点D
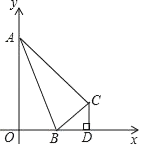
(1)移动点A,发现在某一时刻,△AOB和以点B、D、C为顶点的三角形相似,求这一时刻点C的坐标;
(2)移动点A,当![]() 时求点C的坐标.
时求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
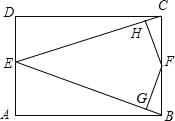
【题目】如图,在矩形ABCD中,AB=3,BC=2,点E为AD中点,点F为BC边上任一点,过点F分别作EB,EC的垂线,垂足分别为点G,H,则FG+FH为( ).
A.![]() B.
B.![]()
![]() C.
C.![]()
![]() D.
D.![]()
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
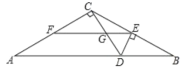
【题目】如图,已知EF是△ABC的中位线,DE⊥BC交AB于点D,CD与EF交于点G,若CD⊥AC,EF=8,EG=3,则AC的长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=kx+b的图象与反比例函数![]() 的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
的图象交于A,B两点,且点A的横坐标和点B的纵坐标都是﹣2,
求:(1)一次函数的解析式;
(2)△AOB的面积;
(3)直接写出一次函数的函数值大于反比例函数的函数值时x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
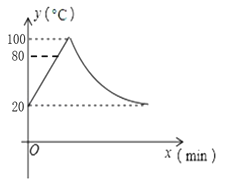
【题目】某品牌的饮水机的运作程序:开机后,20℃的水经过热交换器吸收热能,以每分钟上升6℃的速度加热到80℃,再进入开水器,以每分钟上升10℃的速度从80℃加热到100℃,停止加热,水温下降,此时水温与开机后用时成反比例关系,直至水温降至20℃,开机后进入此程序的整个过程中,水温y(℃)与开机后用时x(min)之间的函数图象如图所示,求在这个过程中:
(1)水温第一次达到80℃的时间;
(2)经过热交换器过程中,y关于x的函数表达式与水温下降过程中,y关于x的函数表达式;
(3)水温不低于20℃且不超过50℃的时间段.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com