
【题目】如图,长度为5的动线段AB分别与坐标系横轴、纵轴的正半轴交于点A、点B,点O和点C关于AB对称,连接CA、CB,过点C作x轴的垂线段CD,交x轴于点D
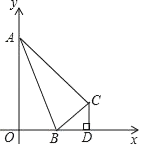
(1)移动点A,发现在某一时刻,△AOB和以点B、D、C为顶点的三角形相似,求这一时刻点C的坐标;
(2)移动点A,当![]() 时求点C的坐标.
时求点C的坐标.
【答案】(1)点![]() 的坐标为
的坐标为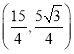 ;(2)
;(2)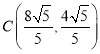 .
.
【解析】
(1)根据轴对称的性质得:AB是OC的垂直平分线,由垂直平分线的性质得:OB=BC,OA=AC,△AOB和以点B、D、C为顶点的三角形相似,存在两种情况:
①当∠ABO=∠CBD时,②当∠ABO=∠BCD时,根据角的关系分别计算点C的坐标即可;
(2)先根据三角函数定义求OB=![]() ,OA=2
,OA=2![]() ,利用面积法得OG和OC的长,根据等角的三角函数可知:OG=2BG,证明△BGO∽△CDO,列比例式可得结论.
,利用面积法得OG和OC的长,根据等角的三角函数可知:OG=2BG,证明△BGO∽△CDO,列比例式可得结论.
(1)连接![]() ,交
,交![]() 于
于![]() ,
,
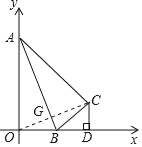
∵点![]() 和点
和点![]() 关于
关于![]() 对称,
对称,
![]() 是
是![]() 的垂直平分线,
的垂直平分线,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 和以点
和以点![]() 为顶点的三角形相似,存在两种情况:
为顶点的三角形相似,存在两种情况:
①当![]() 时,
时,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
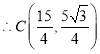 ;
;
②当![]() 时,
时,![]() ,
,
![]() ,
,
![]() 轴,
轴,
![]() 轴,此种情况不成立;
轴,此种情况不成立;
综上所述,![]() 和以点
和以点![]() 为顶点的三角形相似,这一时刻点
为顶点的三角形相似,这一时刻点![]() 的坐标为
的坐标为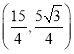 ;
;
(2)![]() ,
,
设![]() ,则
,则![]() ,
,
![]() ,
,
![]() 或
或![]() (舍),
(舍),
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
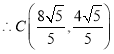 .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(5,0)、C(0,﹣5)三点.
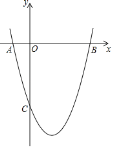
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<5时,y的取值范围为 ;
(3)点P为抛物线上一点,若S△PAB=21,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长沙市计划聘请甲、乙两个工程队对桂花公园进行绿化.已知甲队每天能完成绿化的面积是乙队的2倍;若两队分别各完成300m2的绿化时,甲队比乙队少用3天.

(1)求甲、乙两工程队每天能完成的绿化的面积;
(2)该项绿化工程中有一块长为20m,宽为8m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56m2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M,

求证:(1)△AME∽△BAE;(2)BD2=AD×DM.
查看答案和解析>>
科目:初中数学 来源: 题型:
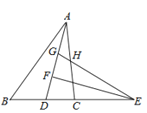
【题目】如图,在![]() 中,4AB=5AC,AD为
中,4AB=5AC,AD为![]() 的角平分线,点E在BC的延长线上,
的角平分线,点E在BC的延长线上,![]() 于点F,点G在AF上,FG=FD,连接EG交AC于点H,若点H是AC的中点,则
于点F,点G在AF上,FG=FD,连接EG交AC于点H,若点H是AC的中点,则![]() 的值为___________
的值为___________
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,点E,F分别是DC和BC两边上的动点且始终保持∠EAF=45°,连接AE与AF交DB于点N,M.下列结论:①△ADM∽△NBA;②△CEF的周长始终保持不变其值是4;③AE×AM=AF×AN;④DN2+BM2=NM2.其中正确的结论是( )
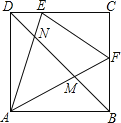
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列网格图中,每个小正方形的边长均为1个单位.在Rt△ABC中,∠C=90°,AC=3,BC=2.
(1)试在图中画出将△ABC以B为旋转中心,沿顺时针方向旋转90°后的图形△A1BC1;
(2)若点B的坐标为(-1,-4),点C的坐标为(-3,-4),试在图中画出直角坐标系,并写出点A的坐标;
(3)根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠A=100°,E,F分别是边AB和BC的中点,EP⊥CD于点P,则∠FPC=( )
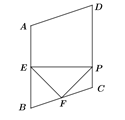
A. 55°B. 65°C. 50°D. 45°
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com