
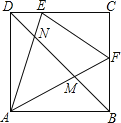
【题目】如图,正方形ABCD的边长为2,点E,F分别是DC和BC两边上的动点且始终保持∠EAF=45°,连接AE与AF交DB于点N,M.下列结论:①△ADM∽△NBA;②△CEF的周长始终保持不变其值是4;③AE×AM=AF×AN;④DN2+BM2=NM2.其中正确的结论是( )
A. ①②③B. ①②④C. ②③④D. ①③④
【答案】B
【解析】
①根据题意证明∠ANB=∠MAD,又因为∠ADM=∠ABN=45°,由AA证明△ADM∽△NBA;
②把△ADE顺时针旋转90°得到△ABG,证明△AEF≌△AGF,得到DG=EF,求出△CEF的周长;
③根据平行线的性质判断即可;
④把△ADN顺时针旋转90°得到△ABH,证明△NAM≌△HAM,根据勾股定理证明结论.
解:①∠ANB=∠NDA+∠NAD=45°+∠NAD,∠MAD=∠MAN+∠NAD=45°+∠NAD,
∴∠ANB=∠MAD,又∠ADM=∠ABN=45°,
∴△ADM∽△NBA,①正确;
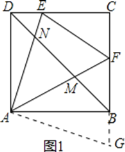
②如图1,把△ADE顺时针旋转90°得到△ABG,则BG=DE,∠FAG=∠FAB+∠DAE=45°,
在△AEF和△AGF中,![]()
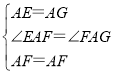 ,
,
∴△AEF≌△AGF,
∴FG=EF,
∴△CEF的周长=CE+CF+EF=CE+DE+CF+FB=4,②正确;
③当MN∥EF时,AE×AM=AF×AN,
∵MN与EF的位置关系不确定,∴③错误;
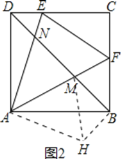
④如图2,把△ADN顺时针旋转90°得到△ABH,则BH=DN,∠ABH=∠AND=45°,∠MAH=∠MAB+∠BAH=∠MAB+∠DAN=45°,
在△NAM和△HAM中,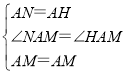 ,
,
∴△NAM≌△HAM,
∴MN=MH,
又∵∠MBH=∠MBA+∠ABH=90°,
∴BH2+BM2=MH2,即DN2+BM2=NM2,④正确.
故选:B.


科目:初中数学 来源: 题型:
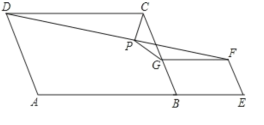
【题目】如图,在平行四边形ABCD和平行四边形BEFG中,AB=AD,BG=BE,点A、 B、 E在同一直线上,P是线段DF的中点,连接PG、PC,若∠ABC=∠BEF=60°,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,矩形ABCD的对角线AC的垂直平分线EF与AD、AC、BC分别交于点E、O、F.
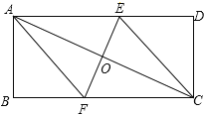
(1)求证:四边形AFCE是菱形;
(2)若AB=5,BC=12,EF=6,求菱形AFCE的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,长度为5的动线段AB分别与坐标系横轴、纵轴的正半轴交于点A、点B,点O和点C关于AB对称,连接CA、CB,过点C作x轴的垂线段CD,交x轴于点D
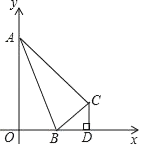
(1)移动点A,发现在某一时刻,△AOB和以点B、D、C为顶点的三角形相似,求这一时刻点C的坐标;
(2)移动点A,当![]() 时求点C的坐标.
时求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt![]() 中,AB=BC=4,
中,AB=BC=4,![]() ,将一直角三角板的直角顶点放在斜边AC的中点P处,将三角板绕点P旋转,三角板的两直角边分别与边AB、BC或其延长线上交于D、E两点(假设三角板的两直角边足够长),如图(1)、图(2)表示三角板旋转过程中的两种情形.
,将一直角三角板的直角顶点放在斜边AC的中点P处,将三角板绕点P旋转,三角板的两直角边分别与边AB、BC或其延长线上交于D、E两点(假设三角板的两直角边足够长),如图(1)、图(2)表示三角板旋转过程中的两种情形.
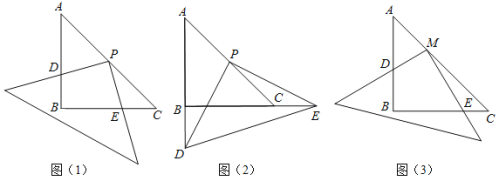
(1)直角三角板绕点P旋转过程中,当![]() ______时,
______时,![]() 是等腰三角形;
是等腰三角形;
(2)直角三角板绕点P旋转到图(1)的情形时,求证:PD=PE;
(3)如图(3),若将直角三角板的顶点放在斜边AC的点M处,设![]() (
(![]() 、
、![]() 为正数),求证:
为正数),求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
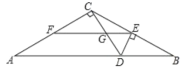
【题目】如图,已知EF是△ABC的中位线,DE⊥BC交AB于点D,CD与EF交于点G,若CD⊥AC,EF=8,EG=3,则AC的长为___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABD中,∠ABD=90°,E为AD的中点,AD∥BC,BE∥CD.
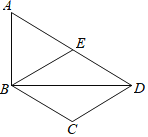
(1)求证:四边形BCDE是菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,已知三角形ABC的边AB是⊙O的切线,切点为B.AC经过圆心O并与圆相交于点D、C,过C作直线CE丄AB,交AB的延长线于点E.

(1)求证:CB平分∠ACE;
(2)若BE=3,CE=4,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
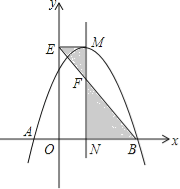
【题目】如图,抛物线![]() 与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
与x轴交于A,B两点,它们的对称轴与x轴交于点N,过顶点M作ME⊥y轴于点E,连结BE交MN于点F.已知点A的坐标为(﹣1,0).
(1)求该抛物线的解析式及顶点M的坐标;
(2)求△EMF与△BNF的面积之比.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com