
【题目】在Rt![]() 中,AB=BC=4,
中,AB=BC=4,![]() ,将一直角三角板的直角顶点放在斜边AC的中点P处,将三角板绕点P旋转,三角板的两直角边分别与边AB、BC或其延长线上交于D、E两点(假设三角板的两直角边足够长),如图(1)、图(2)表示三角板旋转过程中的两种情形.
,将一直角三角板的直角顶点放在斜边AC的中点P处,将三角板绕点P旋转,三角板的两直角边分别与边AB、BC或其延长线上交于D、E两点(假设三角板的两直角边足够长),如图(1)、图(2)表示三角板旋转过程中的两种情形.
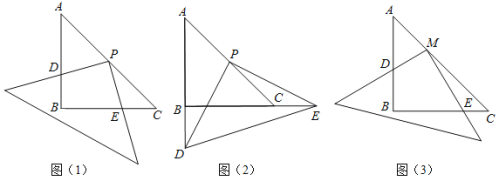
(1)直角三角板绕点P旋转过程中,当![]() ______时,
______时,![]() 是等腰三角形;
是等腰三角形;
(2)直角三角板绕点P旋转到图(1)的情形时,求证:PD=PE;
(3)如图(3),若将直角三角板的顶点放在斜边AC的点M处,设![]() (
(![]() 、
、![]() 为正数),求证:
为正数),求证:![]() .
.
【答案】(1)0,2,![]() 或
或![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(1)根据△PEC是等腰三角形,分类进行讨论即可;
(2)连接BP,首先根据题干条件证明出∠BPD=∠CPE,然后证明△DPB≌△EPC,于是证明出PD=PE;
(3)过M分别作AB、BC的垂线,垂足分别为G、H,首先根据角之间的关系求出∠GMD=∠HME,进而证明出△MGD∽△MHE,根据相似三角形对应边成比例,得到![]() ,再求出GM、HM关于m、n的表达式,三式结合求出MD、ME之间的比例关系.
,再求出GM、HM关于m、n的表达式,三式结合求出MD、ME之间的比例关系.
解:(1)当BE=0时,即点B和点E重合,故可知△PEC是等腰三角形,
当BE=2时,即E是BC的中点,可得△PEC是等腰三角形
由题干条件知PC=![]() ,当CP=CE时△PEC是等腰三角形,BE=4
,当CP=CE时△PEC是等腰三角形,BE=4![]() ;
;
当E在BC的延长线上时,CE=CP,△PEC是等腰三角形,BE=4+![]() ;
;
故答案为:0或2或4![]() 或4+
或4+![]() ;
;
(2)连接BP.
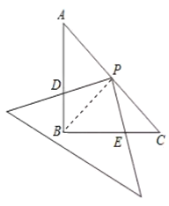
∵AB=BC 且∠ABC=90°,
∴∠C=45°,
又∵P是AC中点,
∴BP⊥AC,BP=PC 且∠ABP=∠CBP=45°,
∴∠CPE+∠EPB=90°,
∵DP⊥PE,
∴∠BPD+∠EPB=90°,
∴∠BPD=∠CPE,
在△DPB和△EPC中,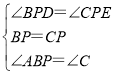 ,
,
∴△DPB≌△EPC,
∴PD=PE;
(3)过M分别作AB、BC的垂线,垂足分别为G、H.
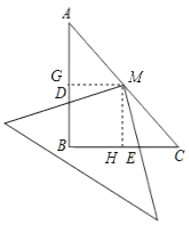
由作图知,∠MGA=∠MGB=∠MHB=∠MHE=90°
又∵∠B=90°,
∴∠GMH=90°,
∴∠GMD+∠DMH=90°,
∵∠DMH+∠HME=90°,
∴∠GMD=∠HME
∴△MGD∽△MHE,
∴![]() ①,
①,
∵![]() ,
,
∴![]() ,
,
∵∠MGA=∠B=90°,
∴GM∥BC,
∴![]() ,即GM=BC
,即GM=BC![]() ②
②
同理 HM=AB![]() ,
,
∵AB=BC,
∴HM=BC![]() ③
③
②③代入①得:![]() .
.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案 天天练口算系列答案
天天练口算系列答案科目:初中数学 来源: 题型:
【题目】某同学练习推铅球,铅球推出后在空中飞行的轨迹是一条抛物线,铅球在离地面1米高的A处推出,达到最高点B时的高度是2.6米,推出的水平距离是4米,铅球在地面上点C处着地
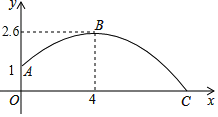
(1)根据如图所示的直角坐标系求抛物线的解析式;
(2)这个同学推出的铅球有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2+4交x轴于A,B两点,顶点是C.
(1)求△ABC的面积;
(2)若点P在抛物线y=-x2+4上, 且S△PAB=![]() S△ABC,求点P的坐标。
S△ABC,求点P的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC是等边三角形,点D、E分别在BC,AC且BD=CE,AD、BE相交于点M,

求证:(1)△AME∽△BAE;(2)BD2=AD×DM.
查看答案和解析>>
科目:初中数学 来源: 题型:
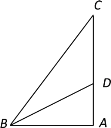
【题目】如图,在Rt△ABC中,∠BAC=90,sinC=![]() ,AC=8,BD平分∠ABC交边AC于点D.
,AC=8,BD平分∠ABC交边AC于点D.
求(1)边AB的长;
(2)tan∠ABD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为2,点E,F分别是DC和BC两边上的动点且始终保持∠EAF=45°,连接AE与AF交DB于点N,M.下列结论:①△ADM∽△NBA;②△CEF的周长始终保持不变其值是4;③AE×AM=AF×AN;④DN2+BM2=NM2.其中正确的结论是( )
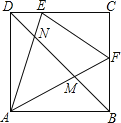
A. ①②③B. ①②④C. ②③④D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
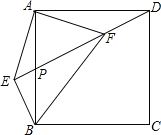
【题目】如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP交DP的延长线于点E,连接AE,过A点作AF⊥AE交DP于点F,连接BF,若AE=2,正方形ABCD的面积为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
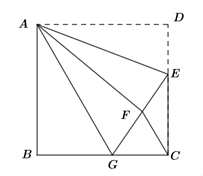
【题目】如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE.将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连结AG、CF.下列结论:
①△ABG≌△AFG;②BG=GC;③AG∥CF;④![]() .
.
其中正确结论的个数是( )
A. 4B. 3C. 2D. 1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com