
【题目】某同学练习推铅球,铅球推出后在空中飞行的轨迹是一条抛物线,铅球在离地面1米高的A处推出,达到最高点B时的高度是2.6米,推出的水平距离是4米,铅球在地面上点C处着地
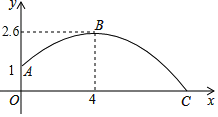
(1)根据如图所示的直角坐标系求抛物线的解析式;
(2)这个同学推出的铅球有多远?
【答案】(1)抛物线的解析式为:y=﹣0.1(x﹣4)2+2.6;(2)这个同学推出的铅球有(![]() +4)米远.
+4)米远.
【解析】
(1)设抛物线的解析式为y=a(x﹣4)2+2.6,由待定系数法求出其解即可;
(2)当y=0时代入(1)的解析式,求出其解即可.
解:(1)设抛物线的解析式为y=a(x﹣4)2+2.6,
由题意,得1=a(0﹣4)2+2.6,
解得:a=﹣0.1.
故y=﹣0.1(x﹣4)2+2.6.
∴抛物线的解析式为:y=﹣0.1(x﹣4)2+2.6;
(2)由题意,得,当y=0时,﹣0.1(x﹣4)2+2.6=0,
解得:x1=![]() +4,x2=﹣
+4,x2=﹣![]() +4<0(舍去),
+4<0(舍去),
故x=![]() +4.
+4.
答:这个同学推出的铅球有(![]() +4)米远.
+4)米远.


科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程(x﹣3)(x﹣2)=|m|.
(1)求证:对于任意实数m,方程总有两个不相等的实数根;
(2)若方程的一个根是1,求m的值及方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
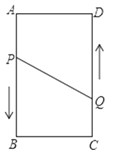
【题目】如图,A、B、C、D为矩形的四个顶点,AB=16cm,AD=6cm,动点P、Q分别从点A、C同时出发,点P以3cm/s的速度向点B移动,一直到达B为止,点Q以2 cm/s的速度向D移动.
(1)P、Q两点从出发开始到几秒?四边形PBCQ的面积为33cm2;
(2)P、Q两点从出发开始到几秒时?点P和点Q的距离是10cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
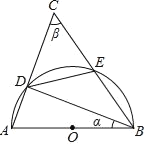
【题目】如图,以△ABC的一边AB为直径的半圆与边AC,BC分别交于点D,E,且弧DE=弧BE,设∠ABD=α,∠C=β.
(1)用含β的代数式表示α,并直接写出β的取值范围;
(2)若AB=10,BC=12,求点O到弦BE的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A的坐标为(0,7),点B的坐标为(0,3),点C的坐标为(3,0).

(1)在图中作出△ABC的外接圆(保留必要的作图痕迹,不写作法),圆心坐标为 ______;
(2)若在x轴的正半轴上有一点D,且∠ADB=∠ACB,则点D的坐标为 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
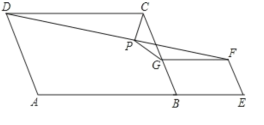
【题目】如图,在平行四边形ABCD和平行四边形BEFG中,AB=AD,BG=BE,点A、 B、 E在同一直线上,P是线段DF的中点,连接PG、PC,若∠ABC=∠BEF=60°,则![]() =( )
=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套,设销售单价为x(x60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单价为多少元时,且销售额为14000元?
(3)当销售单价为多少元时,才能在一个月内获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=ax2+bx+c(a≠0)的图象如图,给出下列4个结论:①abc>0; ②b2>4ac; ③4a+2b+c>0;④2a+b=0.其中正确的有( )个.
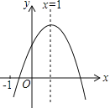
A. 1B. 2C. 3D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt![]() 中,AB=BC=4,
中,AB=BC=4,![]() ,将一直角三角板的直角顶点放在斜边AC的中点P处,将三角板绕点P旋转,三角板的两直角边分别与边AB、BC或其延长线上交于D、E两点(假设三角板的两直角边足够长),如图(1)、图(2)表示三角板旋转过程中的两种情形.
,将一直角三角板的直角顶点放在斜边AC的中点P处,将三角板绕点P旋转,三角板的两直角边分别与边AB、BC或其延长线上交于D、E两点(假设三角板的两直角边足够长),如图(1)、图(2)表示三角板旋转过程中的两种情形.
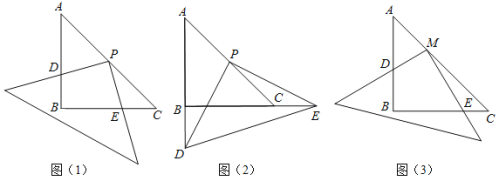
(1)直角三角板绕点P旋转过程中,当![]() ______时,
______时,![]() 是等腰三角形;
是等腰三角形;
(2)直角三角板绕点P旋转到图(1)的情形时,求证:PD=PE;
(3)如图(3),若将直角三角板的顶点放在斜边AC的点M处,设![]() (
(![]() 、
、![]() 为正数),求证:
为正数),求证:![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com