
【题目】如图,在正方形ABCD中,点P是AB的中点,连接DP,过点B作BE⊥DP交DP的延长线于点E,连接AE,过A点作AF⊥AE交DP于点F,连接BF,若AE=2,正方形ABCD的面积为___.
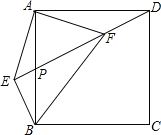
【答案】10
【解析】
如图,由正方形性质和已知就可以得出∠EAF=∠DAB=90°,AB=AD,可以得出∠1=∠2,由对顶角相等可以得出∠5=∠6,所以∠3=∠4,从而可以证明△AEB≌△AFD,可以求得AE=AF,再利用勾股定理就可以求出EF的值,过点A作AM⊥EF于M,由△AEF是等腰直角三角形,可以得出∠AME=90°,由已知可以证明△AMP≌△BEP,可以得出BE=AM=![]() ,最后由勾股定理求出结论.
,最后由勾股定理求出结论.
解:∵四边形ABCD是正方形,且BE⊥DP,AF⊥AE,
∴AB=AD,∠BAD=∠EAF=∠BEF=90°,
∴∠1+∠FAB=∠2+∠FAB=90°,
∴∠1=∠2.
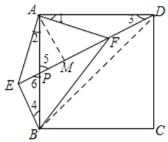
∵∠3+∠5=∠4+∠6,且∠5=∠6,
∴∠3=∠4.
在△AEB和△AFD中,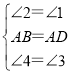 ,
,
∴△AEB≌△AFD(ASA),
∴AE=AF=2,BE=DF,
∴△EAF为等腰直角三角形.
在Rt△EAF中,由勾股定理,得
EF=![]() =2
=2![]() .
.
过点A作AM⊥EF于M,连接BD,
∴AM=MF=EM=![]() EF=
EF=![]() ,∠AME=∠BEF=90°,
,∠AME=∠BEF=90°,
∵点P是AB的中点,
∴AP=BP,
在△AMP和△BEP中, ,
,
∴△AMP≌△BEP(AAS),
∴BE=AM=DF=![]() ,
,
∴DE=EF+DF=2![]() +
+![]() =3
=3![]() ,
,
在Rt△BED中,BD=![]() =
=![]() =
=![]() =2
=2![]() ,
,
∴S正方形ABCD=![]() BD2=
BD2=![]() ×(2
×(2![]() )2=10.
)2=10.
故答案为:10.


 金钥匙试卷系列答案
金钥匙试卷系列答案科目:初中数学 来源: 题型:
【题目】在2014年巴西世界杯足球赛前夕,某体育用品店购进一批单价为40元的球服,如果按单价60元销售,那么一个月内可售出240套,根据销售经验,提高销售单价会导致销售量的减少,即销售单价每提高5元,销售量相应减少20套,设销售单价为x(x60)元,销售量为y套.
(1)求出y与x的函数关系式;
(2)当销售单价为多少元时,且销售额为14000元?
(3)当销售单价为多少元时,才能在一个月内获得最大利润,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数![]() 的顶点P的横坐标为
的顶点P的横坐标为![]() ,且与y轴交于点C(0,-4).
,且与y轴交于点C(0,-4).
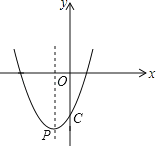
(1)求b,c的值;
(2)直线y=m(m>0)与该抛物线的交点为M,N(点M在点N的左侧)点M关于y轴的对称点为点M,点H的坐标为(3,0).若四边形ONMH的面积为18.求点H到OM的距离;
(3)是否在对称轴的同侧存在实数m、n(m<n),当![]() 时,y的取值范围为
时,y的取值范围为![]() ?若存在,求出m,n的值;若不存在,说明理由.
?若存在,求出m,n的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt![]() 中,AB=BC=4,
中,AB=BC=4,![]() ,将一直角三角板的直角顶点放在斜边AC的中点P处,将三角板绕点P旋转,三角板的两直角边分别与边AB、BC或其延长线上交于D、E两点(假设三角板的两直角边足够长),如图(1)、图(2)表示三角板旋转过程中的两种情形.
,将一直角三角板的直角顶点放在斜边AC的中点P处,将三角板绕点P旋转,三角板的两直角边分别与边AB、BC或其延长线上交于D、E两点(假设三角板的两直角边足够长),如图(1)、图(2)表示三角板旋转过程中的两种情形.
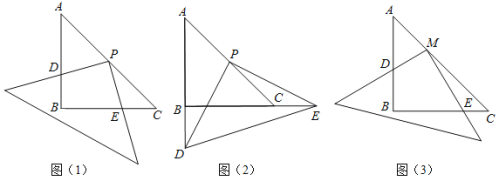
(1)直角三角板绕点P旋转过程中,当![]() ______时,
______时,![]() 是等腰三角形;
是等腰三角形;
(2)直角三角板绕点P旋转到图(1)的情形时,求证:PD=PE;
(3)如图(3),若将直角三角板的顶点放在斜边AC的点M处,设![]() (
(![]() 、
、![]() 为正数),求证:
为正数),求证:![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABD中,∠ABD=90°,E为AD的中点,AD∥BC,BE∥CD.
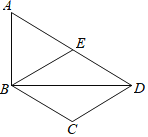
(1)求证:四边形BCDE是菱形;
(2)连接AC,若AC平分∠BAD,BC=1,求AC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的方程x2+(2k-1)x+k2-1=0有两个实数根x1,x2.
(1)求实数k的取值范围;
(2)若x1,x2满足x12+x22=16+x1x2,求实数k的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店销售面向中考生的计数跳绳,每根成本为20元,销售的前40天内的日销售量m(根)与时间t(天)的关系如表.
时间t(天) | 1 | 3 | 8 | 10 | 26 | … |
日销售量m(件) | 51 | 49 | 44 | 42 | 26 | … |
前40天每天的价格y(元/件)与时间t(天)的函数关系式为:y=![]() t+25(1≤t≤40且t为整数);
t+25(1≤t≤40且t为整数);
(1)认真分析表中的数据,用所学过的知识确定m(件)与t(天)之间是满足一次函数的关系还是二次函数的关系?并利用这些数据求m(件)与t(天)之间得函数关系式;
(2)请计算40天中哪一天的日销售利润最大,最大日销售利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】要建一个面积为150平方米的长方形养鸡场,为了节约材料,鸡场一边靠着原有的一堵墙,墙长为18米,另三边用篱笆围成,如篱笆长度为35米,且要求用完。求鸡场的长与宽各是多少米?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com