
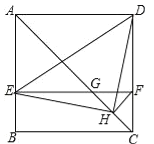
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作EF∥AD,与AC、DC分别交于点G,F,H为CG的中点,连接DE,EH,DH,FH.下列结论:①EG=DF;②∠AEH+∠ADH=180°;③△EHF≌△DHC;④若![]() ,则3S△EDH=13S△DHC,其中结论正确的序号有__.
,则3S△EDH=13S△DHC,其中结论正确的序号有__.
【答案】①②③④
【解析】
①根据题意可知∠ACD=45°,则GF=FC,则EG=EF-GF=CD-FC=DF;
②由SAS证明△EHF≌△DHC,得到∠HEF=∠HDC,从而∠AEH+∠ADH=∠AEF+∠HEF+∠ADF-∠HDC=180°;
③同②证明△EHF≌△DHC即可;
④若![]() ,则AE=2BE,可以证明△EGH≌△DFH,则∠EHG=∠DHF且EH=DH,则∠DHE=90°,△EHD为等腰直角三角形,过H点作HM垂直于CD于M点,设HM=x,则DM=5x,DH=
,则AE=2BE,可以证明△EGH≌△DFH,则∠EHG=∠DHF且EH=DH,则∠DHE=90°,△EHD为等腰直角三角形,过H点作HM垂直于CD于M点,设HM=x,则DM=5x,DH=![]() x,CD=6x,则S△DHC=
x,CD=6x,则S△DHC=![]() ×HM×CD=3x2,S△EDH=
×HM×CD=3x2,S△EDH=![]() ×DH2=13x2.
×DH2=13x2.
①∵四边形ABCD为正方形,EF∥AD,
∴EF=AD=CD,∠ACD=45°,∠GFC=90°,
∴△CFG为等腰直角三角形,
∴GF=FC,
∵EG=EF-GF,DF=CD-FC,
∴EG=DF,故①正确;
②∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=CH,∠GFH=![]() ∠GFC=45°=∠HCD,
∠GFC=45°=∠HCD,
在△EHF和△DHC中,
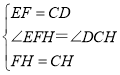 ,
,
∴△EHF≌△DHC(SAS),
∴∠HEF=∠HDC,
∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF-∠HDC=∠AEF+∠ADF=180°,故②正确;
③∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=CH,∠GFH=![]() ∠GFC=45°=∠HCD,
∠GFC=45°=∠HCD,
在△EHF和△DHC中,
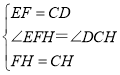
∴△EHF≌△DHC(SAS),故③正确;
④∵![]() ,
,
∴AE=2BE,
∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=GH,∠FHG=90°,
∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD,
在△EGH和△DFH中,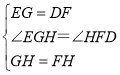 ,
,
∴△EGH≌△DFH(SAS),
∴∠EHG=∠DHF,EH=DH,∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°,
∴△EHD为等腰直角三角形,
过H点作HM垂直于CD于M点,如图所示:
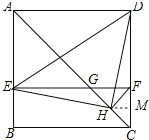
设HM=x,则DM=5x,DH=![]() x,CD=6x,
x,CD=6x,
则S△DHC=![]() ×HM×CD=3x2,S△EDH=
×HM×CD=3x2,S△EDH=![]() ×DH2=13x2,
×DH2=13x2,
∴![]()
∴3S△EDH=13S△DHC,故④正确;
故答案为:①②③④


 小学课时特训系列答案
小学课时特训系列答案科目:初中数学 来源: 题型:
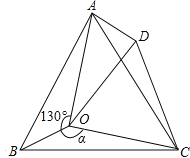
【题目】如图,点O是等边三角形ABC内的一点,∠AOB=130°,∠BOC=α.将△BOC绕点C按顺时针方向旋转60°得到△ADC,连接OD.
(1)判断△COD的形状,并加以说明理由.
(2)若AD=1,OC=![]() ,OA=
,OA=![]() 时,求α的度数.
时,求α的度数.
(3)探究:当α为多少度时,△AOD是等腰三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,△OBA和△DOC的边OA、OC都在x轴的正半轴上,点B的坐标为(6,8),∠BAO![]() ∠OCD
∠OCD![]() 90°,OD
90°,OD![]() 5,CD
5,CD![]() 3.反比例函数
3.反比例函数![]() 的图象经过点D,交AB边于点E.
的图象经过点D,交AB边于点E.

(1)求k的值;(2)求BE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
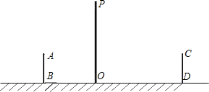
【题目】如图,是小亮晚上在广场散步的示意图,图中线段![]() 表示站立在广场上的小亮,线段
表示站立在广场上的小亮,线段![]() 表示直立在广场上的灯杆,点
表示直立在广场上的灯杆,点![]() 表示照明灯的位置.
表示照明灯的位置.
![]() 在小亮由
在小亮由![]() 处沿
处沿![]() 所在的方向行走到达
所在的方向行走到达![]() 处的过程中,他在地面上的影子长度越来越________(用“长”或“短”填空);请你在图中画出小亮站在
处的过程中,他在地面上的影子长度越来越________(用“长”或“短”填空);请你在图中画出小亮站在![]() 处的影子
处的影子![]() ;
;
![]() 当小亮离开灯杆的距离
当小亮离开灯杆的距离![]() 时,身高为
时,身高为![]() 的小亮的影长为
的小亮的影长为![]() ,
,
①灯杆的高度为多少![]() ?
?
②当小亮离开灯杆的距离![]() 时,小亮的影长变为多少
时,小亮的影长变为多少![]() ?
?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB过点A(3,0),B(0,2)
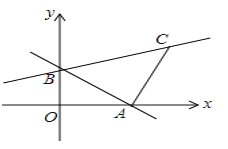
(1)求直线AB的解析式。
(2)过点A作AC⊥AB且AC∶AB=3∶4,求过B、C两点直线的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=ax2+bx+c经过A(﹣1,0)、B(5,0)、C(0,﹣5)三点.
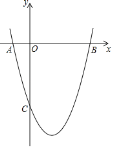
(1)求抛物线的解析式和顶点坐标;
(2)当0<x<5时,y的取值范围为 ;
(3)点P为抛物线上一点,若S△PAB=21,直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】长沙市计划聘请甲、乙两个工程队对桂花公园进行绿化.已知甲队每天能完成绿化的面积是乙队的2倍;若两队分别各完成300m2的绿化时,甲队比乙队少用3天.

(1)求甲、乙两工程队每天能完成的绿化的面积;
(2)该项绿化工程中有一块长为20m,宽为8m的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为56m2,两块绿地之间及周边留有宽度相等的人行通道(如图所示),问人行通道的宽度是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列网格图中,每个小正方形的边长均为1个单位.在Rt△ABC中,∠C=90°,AC=3,BC=2.
(1)试在图中画出将△ABC以B为旋转中心,沿顺时针方向旋转90°后的图形△A1BC1;
(2)若点B的坐标为(-1,-4),点C的坐标为(-3,-4),试在图中画出直角坐标系,并写出点A的坐标;
(3)根据(2)的坐标系作出与△ABC关于原点对称的图形△A2B2C2.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com