
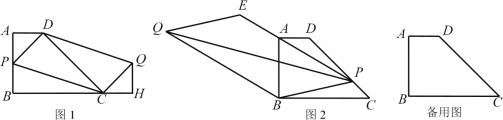
【题目】已知在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=4,BC=6.
(1)如图1,P为AB边上一点,以PD,PC为边作平行四边形PCQD,过点Q作QH⊥BC,交BC的延长线于H.求证:△ADP≌△HCQ;
(2)若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作平行四边形PCQE.请问对角线PQ的长是否存在最小值?如果存在,请求出最小值;如果不存在,请说明理由.
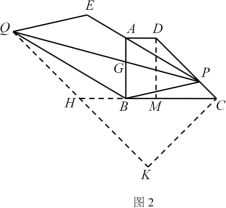
(3)如图2,若P为DC边上任意一点,延长PA到E,使AE=nPA(n为常数),以PE,PB为边作平行四边形PBQE.请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值;如果不存在,请说明理由.
【答案】(1)见解析;(2)存在最小值,最小值为10;(3)存在最小值,最小值为 ![]() ( n+4 ).
( n+4 ).
【解析】
(1)首先根据四边形PCQD是平行四边形,可得PD=QC;然后根据全等三角形判定的方法,判断出△APD≌△HQC即可.
(2)设![]() 与
与![]() 相交于点
相交于点![]() ,由平行线得出
,由平行线得出![]() ,得出
,得出![]() 是
是![]() 上一定点,作
上一定点,作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,证明
,证明![]() ,得出
,得出![]() ,求出
,求出![]() 得出
得出![]() ,当
,当![]() 时,
时,![]() 的长最小,即为5.
的长最小,即为5.
(3)设![]() 与
与![]() 相交于点
相交于点![]() ,由平行线得出
,由平行线得出![]() =
=![]() =
=![]() ,作
,作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于
的延长线于![]() ,证明
,证明![]() ,得出
,得出![]() =
=![]() =
=![]() ,求出BH=2(n+1),得出
,求出BH=2(n+1),得出![]() ,过点
,过点![]() 作
作![]() 于
于![]() ,则四边形
,则四边形![]() 是矩形,得出
是矩形,得出![]() ,
,![]() ,证出
,证出![]() ,由三角函数得出CK=CH·cos45°=
,由三角函数得出CK=CH·cos45°=![]() ( 2n+8 )=
( 2n+8 )=![]() ( n+4 ),即可得出结果.
( n+4 ),即可得出结果.
解:(1)∵AD∥BC,
∴∠ADC=∠DCH

即∠ADP+∠PDC=∠DCQ+∠QCH,
∵四边形PCQD是平行四边形,
∴PD∥CQ,PD=CQ,
∴∠PDC=∠DCQ,
∴∠ADP=∠QCH,
又∵PD=CQ,∠A=∠CHQ=90°,
∴△ADP≌△HCQ(AAS)
(2)存在最小值,最小值为10.
如图,设PQ与DC相交于点G,

∵PE∥CQ,易得△DPG∽△CQG,
又PD=DE=![]() PE,PE=CQ,
PE,PE=CQ,
∴![]() =
= ![]() =
= ![]() ,
,
∴G是DC上一定点
作QH⊥BC,交BC的延长线于H
同(1)可证∠ADP=∠QCH
∴Rt△ADP∽Rt△QCH
∴![]() =
= ![]() =
=![]() ,
,
∴CH=4,
∴BH=BC+CH=6+4=10,
∴当PQ⊥AB时,PQ的长最小,即为10.
(3)存在最小值,最小值为 ![]() ( n+4 ).
( n+4 ).
如图,设PQ与AB相交于点G
∵PE∥BQ,AE=nPA,
∴![]() =
=![]() =
=![]() ,
,
∴G是AB上一定点,
作QH∥DC,交CB的延长线于H,作CK⊥CD,交QH的延长线于K,
∵AD∥BC,AB⊥BC,
∴∠ADP=∠BHQ,
∵∠PAD+∠PAG=∠QBH+∠QBG=90°,∠PAG=∠QBG,
∴∠PAD=∠QBH,
∴△ADP∽△BHQ,
∴![]() =
=![]() =
=![]()
∴BH=2(n+1) ,
∴CH=BC+BH=6+2n+2=2n+8,
过点D作DM⊥BC于M,则四边形ABMD是矩形,
∴BM=AD=2,DM=AB=4,
∴MC=BC-BM=6-2=4=DM,
∴∠DCM=45°,
∴∠HCK=45°,
∴CK=CH·cos45°=![]() ( 2n+8 )=
( 2n+8 )=![]() ( n+4 ) ,
( n+4 ) ,
∴当PQ⊥CD时,PQ的长最小,最小值为![]() ( n+4 ).
( n+4 ).


科目:初中数学 来源: 题型:
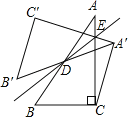
【题目】如图,点D是Rt△ABC斜边AB的中点,点E在边AC上.△A'B′C′与△ABC关于直线BE对称,连结A′C.且∠CA′C'=90°.若AC=4,BC=3.则AE的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:(![]() ﹣1)0+2sin30°-
﹣1)0+2sin30°-![]() +|﹣2017|;
+|﹣2017|;
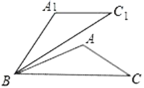
(2)如图,在△ABC中,已知∠ABC=30°,将△ABC绕点B逆时针旋转50°后得到△A1BC1,若∠A=100°,求证:A1C1∥BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
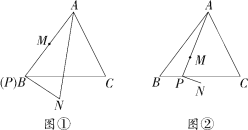
【题目】如图,在△ABC中,AB=BC=10,tan∠ABC=![]() ,点P是边BC上的一点,M是线段AP上一点,线段PM绕点P顺时针旋转90°得线段PN,设BP=t.
,点P是边BC上的一点,M是线段AP上一点,线段PM绕点P顺时针旋转90°得线段PN,设BP=t.
(1)如图①,当点P在点B,点M是AP中点时,试求AN的长;
(2)如图②,当![]() =
=![]() 时,
时,
①求点N到BC边的距离(用含t的代数式表示);
②当点P从点B运动至点C时,试求点N运动路径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
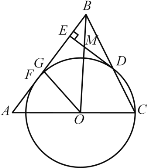
【题目】如图,在△ABC中,AB=AC=10,tan∠A=![]() ,点O是线段AC上一动点(不与点A,点C重合),以OC为半径的⊙O与线段BC的另一个交点为D,作DE⊥AB于E.
,点O是线段AC上一动点(不与点A,点C重合),以OC为半径的⊙O与线段BC的另一个交点为D,作DE⊥AB于E.
(1)求证:DE是⊙O的切线;
(2)当⊙O与AB相切于点F时,求⊙O的半径;
(3)在(2)的条件下,连接OB交DE于点M,点G在线段EF上,连接GO.若∠GOM=45°,求DM和FG的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1是某体育看台侧面的示意图,观众区AC的坡度i=1:2,顶端C离水平地面AB的高度为15m,顶棚外沿处的点E恰好在点A的正上方,从D处看E处的仰角α=30°,竖直的立杆上C,D两点间的距离为5m.
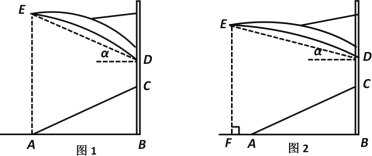
(1)求观众区的水平宽度AB.
(2)求图1中点E离水平地面的高度EA.
(3)因为遮阳需要,现将顶棚ED绕D点逆时针转动11°30′,若E点在地面上的铅直投影是点F(图2),求AF.(sin11°30′≈0.20,cos11°30′≈0.98,tan11°30′≈0.20;sin18°30′≈0.32,cos18°30′≈0.95,tan18°30′≈0.33,结果精确到0.1m)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售一种商品,若将50件该商品按标价打八折销售,比按原标价销售这些商品少获利200元.
![]() 求该商品的标价为多少元;
求该商品的标价为多少元;
![]() 已知该商品的进价为每件12元,根据市场调査:若按
已知该商品的进价为每件12元,根据市场调査:若按![]() 中标价销售,该商场每天销售100件;每涨1元,每天要少卖5件
中标价销售,该商场每天销售100件;每涨1元,每天要少卖5件![]() 那么涨价后要使该商品每天的销售利润最大,应将销售价格定为每件多少元?最大利润是多少?
那么涨价后要使该商品每天的销售利润最大,应将销售价格定为每件多少元?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
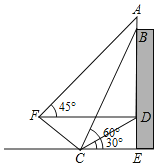
【题目】为积极参与鄂州市全国文明城市创建活动,我市某校在教学楼顶部新建了一块大型宣传牌,如下图.小明同学为测量宣传牌的高度![]() ,他站在距离教学楼底部
,他站在距离教学楼底部![]() 处6米远的地面
处6米远的地面![]() 处,测得宣传牌的底部
处,测得宣传牌的底部![]() 的仰角为
的仰角为![]() ,同时测得教学楼窗户
,同时测得教学楼窗户![]() 处的仰角为
处的仰角为![]() (
(![]() 、
、![]() 、
、![]() 、
、![]() 在同一直线上).然后,小明沿坡度
在同一直线上).然后,小明沿坡度![]() 的斜坡从
的斜坡从![]() 走到
走到![]() 处,此时
处,此时![]() 正好与地面
正好与地面![]() 平行.
平行.
(1)求点![]() 到直线
到直线![]() 的距离(结果保留根号);
的距离(结果保留根号);
(2)若小明在![]() 处又测得宣传牌顶部
处又测得宣传牌顶部![]() 的仰角为
的仰角为![]() ,求宣传牌的高度
,求宣传牌的高度![]() (结果精确到0.1米,
(结果精确到0.1米,![]() ,
,![]() ).
).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com