
【题目】(1)计算:(![]() ﹣1)0+2sin30°-
﹣1)0+2sin30°-![]() +|﹣2017|;
+|﹣2017|;
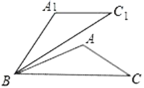
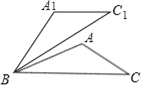
(2)如图,在△ABC中,已知∠ABC=30°,将△ABC绕点B逆时针旋转50°后得到△A1BC1,若∠A=100°,求证:A1C1∥BC.
【答案】(1)2017;(2)见解析
【解析】
(1)原式利用零指数幂的意义、特殊角的三角函数值、负整数指数幂的意义以及绝对值的代数意义计算即可得到结果;
(2)先在△ABC中利用三角形内角和定理求出∠C=50°,再根据旋转的性质求出∠C1=∠C=50°,∠C1BC=50°.等量代换得出∠C1=∠C1BC,根据平行线的判定即可证明A1C1∥BC.
解:(1)原式=1+2×![]() ﹣2+2017
﹣2+2017
=1+1﹣2+2017
=2017;
(2)证明:在△ABC中,∵∠ABC=30°,∠A=100°,
∴∠C=180°﹣∠A﹣∠ABC=50°.
∵将△ABC绕点B逆时针旋转50°后得到△A1BC1,
∴∠C1=∠C=50°,∠C1BC=50°.
∴∠C1=∠C1BC,
∴A1C1∥BC.


科目:初中数学 来源: 题型:
【题目】某工厂要加工甲、乙、丙三种型号机械配件共120个,安排20个工人刚好一天加工完成,每人只加工一种配件,设加工甲种配件的人数为x,加工乙种配件的人数为y,根据下表提供的信息,解答下列问题:
配件种类 | 甲 | 乙 | 丙 |
每人每天加工配件的数量 | 8 | 6 | 5 |
每个配件获利 | 15 | 14 | 8 |
![]() 求y与x之间的关系.
求y与x之间的关系.
![]() 若这些机械配件共获利1420元,请求出加工甲、乙、丙三种型号配件的人数分别是多少人?
若这些机械配件共获利1420元,请求出加工甲、乙、丙三种型号配件的人数分别是多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为开拓学生视野,开展“课外读书周”活动,活动后期随机调查了九年级部分学生一周的课外阅读时间,并将结果绘制成两幅不完整的统计图,请你根据统计图(如图)的信息回答下列问题:
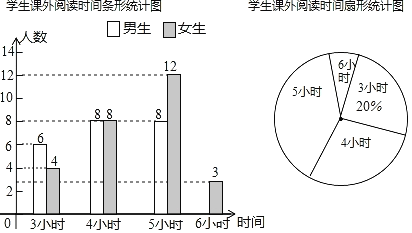
(1)本次调查的学生总数为 人,被调查学生的课外阅读时间的中位数是 小时,众数是 小时;
(2)请你补全条形统计图,在扇形统计图中,课外阅读时间为5小时的扇形的圆心角度数是 ;
(3)若全校九年级共有学生700人,估计九年级一周课外阅读时间为6小时的学生有多少人?
(4)若学校需要,从二男二女四名同学中随机选取两人分享读后感,恰好是一男一女的概率?(列表或树状图)
查看答案和解析>>
科目:初中数学 来源: 题型:
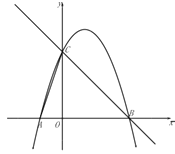
【题目】已知,在平面直角坐标系中,O为坐标原点,抛物线![]() 交
交![]() 轴于
轴于![]() 、
、![]() 两点(
两点(![]() 在
在![]() 轴负半轴上),交
轴负半轴上),交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)![]() 为直线
为直线![]() 上方第一象限内一点,连接
上方第一象限内一点,连接![]() 、
、![]() ,
,![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,设点
,设点![]() 的横坐标为
的横坐标为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() ,求
,求![]() 与
与![]() 之间的函数关系式;(不要求写出自变量
之间的函数关系式;(不要求写出自变量![]() 的取值范围)
的取值范围)
(3)把线段![]() 沿直线
沿直线![]() 翻折,得到线段
翻折,得到线段![]() ,
,![]() 为第二象限内一点,连接
为第二象限内一点,连接![]() 、
、![]() ,
,![]() ,
,![]() 为线段
为线段![]() 上一点,
上一点,![]() 于点
于点![]() ,射线
,射线![]() 交线段
交线段![]() 于点
于点![]() ,连接
,连接![]() 交
交![]() 于
于![]() ,交
,交![]() 于点
于点![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,设直线
,设直线![]() 与抛物线第一象限交点为
与抛物线第一象限交点为![]() ,求点
,求点![]() 坐标.
坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y1=ax2-2amx+am2+4,直线y2=kx-km+4,其中a≠0,a、k、m是常数.
(1)抛物线的顶点坐标是______,并说明上述抛物线与直线是否经过同一点(说明理由);
(2)若a<0,m=2,t≤x ≤t+2,y1的最大值为4,求t的范围;
(3)抛物线的顶点为P,直线与抛物线的另一个交点为Q,对任意的m值,若1≤k≤4,线段PQ(不包括端点)上至少存在两个横坐标为整数的点,求a的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 和抛物线
和抛物线![]() :
:![]() ,其中
,其中![]() .
.
![]() 下列说法你认为正确的序号是______;
下列说法你认为正确的序号是______;
![]() 抛物线
抛物线![]() 和
和![]() 与y轴交于同一点
与y轴交于同一点![]() ;
;
![]() 抛物线
抛物线![]() 和
和![]() 开口都向上;
开口都向上;
![]() 抛物线
抛物线![]() 和
和![]() 的对称轴是同一条直线;
的对称轴是同一条直线;
![]() 当
当![]() 时,抛物线
时,抛物线![]() 和
和![]() 都与x轴有两个交点
都与x轴有两个交点
![]() 抛物线
抛物线![]() 和
和![]() 相交于点E、F,当k的值发生变化时,请判断线段EF的长度是否发生变化,并说明理由;
相交于点E、F,当k的值发生变化时,请判断线段EF的长度是否发生变化,并说明理由;
![]() 在
在![]() 中,若抛物线
中,若抛物线![]() 的顶点为M,抛物线
的顶点为M,抛物线![]() 的顶点为N,问:
的顶点为N,问:
是否存在实数k,使![]() ?如存在,求出实数k;如不存在,请说明理由.
?如存在,求出实数k;如不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4张卡片,卡片上分別标有数字1、﹣2、3、﹣4,这些卡片除数字外都相同.王兴从口袋中随机抽取一张卡片,钟华从剩余的三张卡片中随机抽取一张,求两张卡片上数字之积.
(1)请你用画树状图或列表的方法,列出两人抽到的数字之积所有可能的结果.
(2)求两人抽到的数字之积为正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在四边形ABCD中,AD∥BC,AB⊥BC,AD=2,AB=4,BC=6.
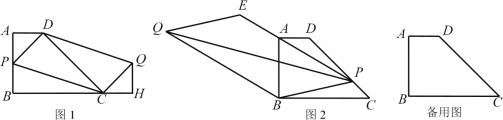
(1)如图1,P为AB边上一点,以PD,PC为边作平行四边形PCQD,过点Q作QH⊥BC,交BC的延长线于H.求证:△ADP≌△HCQ;
(2)若P为AB边上任意一点,延长PD到E,使DE=PD,再以PE,PC为边作平行四边形PCQE.请问对角线PQ的长是否存在最小值?如果存在,请求出最小值;如果不存在,请说明理由.
(3)如图2,若P为DC边上任意一点,延长PA到E,使AE=nPA(n为常数),以PE,PB为边作平行四边形PBQE.请探究对角线PQ的长是否也存在最小值?如果存在,请求出最小值;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
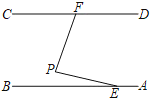
【题目】如图,在同一平面内,两条平行的高速公路AB和CD之间有一条“L”型道路连通,“L”型道路中的EP=FP=20千米,∠BEP=12°,∠EPF=80°,求AB和CD之间的距离.(参考数据:sin12°=cos78°≈0.21,sin68°=cos22°≈0.93,tan68°≈2.48)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com