
ЁОЬтФПЁПвбжЊЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌOЮЊзјБъдЕуЃЌХзЮяЯп![]() НЛ
НЛ![]() жсгк
жсгк![]() ЁЂ
ЁЂ![]() СНЕу(
СНЕу(![]() дк
дк![]() жсИКАыжсЩЯ)ЃЌНЛ
жсИКАыжсЩЯ)ЃЌНЛ![]() жсгкЕу
жсгкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉ![]() ЮЊжБЯп
ЮЊжБЯп![]() ЩЯЗНЕквЛЯѓЯоФквЛЕуЃЌСЌНг
ЩЯЗНЕквЛЯѓЯоФквЛЕуЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ![]() ЃЌбгГЄ
ЃЌбгГЄ![]() НЛ
НЛ![]() жсгкЕу
жсгкЕу![]() ЃЌЩшЕу
ЃЌЩшЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ(ВЛвЊЧѓаДГіздБфСП
жЎМфЕФКЏЪ§ЙиЯЕЪНЃЛ(ВЛвЊЧѓаДГіздБфСП![]() ЕФШЁжЕЗЖЮЇ)
ЕФШЁжЕЗЖЮЇ)
ЃЈ3ЃЉАбЯпЖЮ![]() бижБЯп
бижБЯп![]() ЗелЃЌЕУЕНЯпЖЮ
ЗелЃЌЕУЕНЯпЖЮ![]() ЃЌ
ЃЌ![]() ЮЊЕкЖўЯѓЯоФквЛЕуЃЌСЌНг
ЮЊЕкЖўЯѓЯоФквЛЕуЃЌСЌНг![]() ЁЂ
ЁЂ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЮЊЯпЖЮ
ЮЊЯпЖЮ![]() ЩЯвЛЕуЃЌ
ЩЯвЛЕуЃЌ![]() гкЕу
гкЕу![]() ЃЌЩфЯп
ЃЌЩфЯп![]() НЛЯпЖЮ
НЛЯпЖЮ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() НЛ
НЛ![]() гк
гк![]() ЃЌНЛ
ЃЌНЛ![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌШє
ЃЌШє![]() ЃЌ
ЃЌ![]() ЃЌЩшжБЯп
ЃЌЩшжБЯп![]() гыХзЮяЯпЕквЛЯѓЯоНЛЕуЮЊ
гыХзЮяЯпЕквЛЯѓЯоНЛЕуЮЊ![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() зјБъЃЎ
зјБъЃЎ
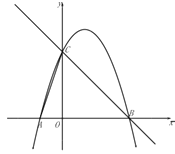
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉ
ЃЛЃЈ3ЃЉ![]() ЃЈ1ЃЌ4ЃЉ
ЃЈ1ЃЌ4ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнХзЮяЯпНтЮіЪН![]() ПЩЧѓЕУЕуCзјБъЃЌдйИљОн
ПЩЧѓЕУЕуCзјБъЃЌдйИљОн![]() ЃЌПЩЧѓЕУЕуAзјБъЃЌдйНЋЕуAзјБъДњШыНтЮіЪНМДПЩЧѓЕУЃЛ
ЃЌПЩЧѓЕУЕуAзјБъЃЌдйНЋЕуAзјБъДњШыНтЮіЪНМДПЩЧѓЕУЃЛ
ЃЈ2ЃЉШчЭМЃЌЙ§ЕуPзїPHЁЭxжсгкHЃЌЙ§ЕуBзїBDЁЭPRЃЌжЄУїЁЯPRB=ЁЯPBRЃЌдђЁїPRBЮЊЕШбќШ§НЧаЮЃЌМДПЩЕУЕНRH=HBЃЌдйДњШыИїЕуКсзјБъМДПЩЧѓЕУЙиЯЕЪНЃЛ
ЃЈ3ЃЉШчЭМЃЌЩш![]() ЃЌдђ
ЃЌдђ![]() ЃЌЫљвд
ЃЌЫљвд![]() ЃЌдђEЃЈЉ1ЃЌ
ЃЌдђEЃЈЉ1ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
гЩ![]() ЃЌЧвBDЮЊЯпЖЮABбижБЯпBCЗелЫљЕУЃЌПЩжЊЕуDЃЈ3ЃЌ4ЃЉЃЌЧѓЕУ
ЃЌЧвBDЮЊЯпЖЮABбижБЯпBCЗелЫљЕУЃЌПЩжЊЕуDЃЈ3ЃЌ4ЃЉЃЌЧѓЕУ![]() ЃЌ
ЃЌ
гЩFNЁЭBEжЊ![]() ЃЌдђ
ЃЌдђ![]() ЃЌПЩЧѓжБЯпFGЕФНтЮіЪНЮЊЃК
ЃЌПЩЧѓжБЯпFGЕФНтЮіЪНЮЊЃК![]() ЃЌНјЖјЧѓЕУ
ЃЌНјЖјЧѓЕУ![]() ЃЌвђЮЊ
ЃЌвђЮЊ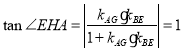 ЃЌДњШыПЩЧѓЕУ
ЃЌДњШыПЩЧѓЕУ![]() ЃЌдђЕуGзјБъЮЊЃЈ3ЃЌ2ЃЉЃЌЫљвджБЯпAGЕФНтЮіЪНЮЊЃК
ЃЌдђЕуGзјБъЮЊЃЈ3ЃЌ2ЃЉЃЌЫљвджБЯпAGЕФНтЮіЪНЮЊЃК![]() ЃЌжБЯпBEЕФНтЮіЪНЮЊЃК
ЃЌжБЯпBEЕФНтЮіЪНЮЊЃК![]() ЃЛдйЩшЕуKЃЈuЃЌ
ЃЛдйЩшЕуKЃЈuЃЌ![]() ЃЉЃЌдђ
ЃЉЃЌдђ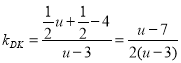 ЃЌ
ЃЌ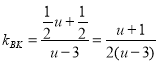 ЃЌгЩ
ЃЌгЩ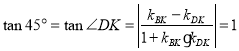 ЃЌНтЕУ
ЃЌНтЕУ![]() ЃЌдђKЃЈ
ЃЌдђKЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌжБЯпBKЕФНтЮіЪНЮЊЃК
ЃЉЃЌжБЯпBKЕФНтЮіЪНЮЊЃК![]() ЃЌгЩЕуMЮЊжБЯпBKгыХзЮяЯпЕФНЛЕуЃЌСЊСЂЗНГЬМДПЩЧѓЕУЕуMЃЈ1ЃЌ4ЃЉЃЎ
ЃЌгЩЕуMЮЊжБЯпBKгыХзЮяЯпЕФНЛЕуЃЌСЊСЂЗНГЬМДПЩЧѓЕУЕуMЃЈ1ЃЌ4ЃЉЃЎ
НтЃКЃЈ1ЃЉгЩХзЮяЯп![]() ПЩжЊЃЌ
ПЩжЊЃЌ
ЕуCЃЈ0ЃЌ3ЃЉЃЌ
ЁрOC=3ЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрOA=1ЃЌ
ЁрAЃЈЉ1ЃЌ0ЃЉЃЌ
НЋЕуAЃЈЉ1ЃЌ0ЃЉДњШы![]() ЃЌ
ЃЌ
ПЩЧѓЕУЃКb=2ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃК![]()
ЃЈ2ЃЉШчЭМЃЌЙ§ЕуPзїPHЁЭxжсгкHЃЌЙ§ЕуBзїBDЁЭPRЃЌ
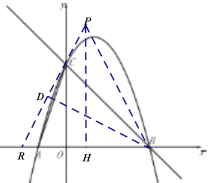
гЩЃЈ1ЃЉжЊХзЮяЯпЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
ЁрПЩЧѓЕУЕуBзјБъЮЊЃЌЃЈ3ЃЌ0ЃЉЃЌ
ЁрOC=OBЃЌ
ЁрЁЯCBO=45ЁуЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрЁЯPBC=ЁЯDBCЃЌ
ЁпЁЯPBR=ЁЯPBCЃЋЁЯCBO=45ЁуЃЋЁЯPBCЃЌЁЯDRB=90ЁуЃЁЯDBRЃЌЖјЁЯDBR=ЁЯCBOЃЁЯDBOЃЌ
ЁрЁЯDRB=90ЁуЃЁЯCBO+ЁЯDBO=45ЁуЃЋЁЯDBOЃЌ
ЁрЁЯPRB=ЁЯPBRЃЌ
ЁрЁїPRBЮЊЕШбќШ§НЧаЮЃЌRH=HBЃЌ
ЁпЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЌЕу
ЃЌЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]()
Ёр![]() ЃЌ
ЃЌ
МД![]() ЃЛ
ЃЛ
ЃЈ3ЃЉШчЭМЃЌ
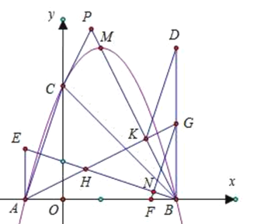
Щш![]() ЃЌдђ
ЃЌдђ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
ЁрEЃЈЉ1ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Ёп![]() ЃЌBDЮЊЯпЖЮABбижБЯпBCЗелЫљЕУЃЌ
ЃЌBDЮЊЯпЖЮABбижБЯпBCЗелЫљЕУЃЌ
ЁрЕуDЃЈ3ЃЌ4ЃЉЃЌ
Ёр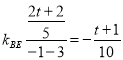 ЃЌ
ЃЌ
ЁпFNЁЭBEЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁржБЯпFGЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
Сю![]() ЃЌдђ
ЃЌдђ![]() ЃЈ3ЃЌ
ЃЈ3ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
Ёр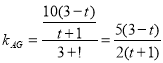
ЁпЁЯEHA=45ЁуЃЌ
гЩжБЯпЕФМаНЧЙЋЪНЕУЃК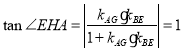 ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЛЏМђЕУЃК![]() ЃЌ
ЃЌ
МД![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрGЃЈ3ЃЌ2ЃЉЃЌ
ЁржБЯпAGЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
ЁржБЯпBEЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
ЩшЕуKЃЈuЃЌ![]() ЃЉЃЌ
ЃЉЃЌ![]() ЃЌ
ЃЌ
Ёр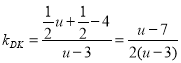 ЃЌ
ЃЌ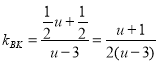 ЃЌ
ЃЌ
гЩжБЯпМаНЧЙЋЪНЕУЃК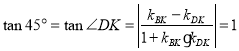 ,
,
МДЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЛЏМђЕУЃК![]() Лђ
Лђ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрKЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЌ
ЃЉЃЌ
ЁржБЯпBKЕФНтЮіЪНЮЊЃК![]() ЃЌ
ЃЌ
ЁпЕуMЮЊжБЯпBKгыХзЮяЯпЕФНЛЕуЃЌ
ЁрСЊСЂ![]() ЃЌ
ЃЌ
НтЕУЃК![]() Лђ
Лђ![]() ЃЈМДЮЊЕуBЃЌЩсШЅЃЉЃЌ
ЃЈМДЮЊЕуBЃЌЩсШЅЃЉЃЌ
ЫљвдЕуMЃЈ1ЃЌ4ЃЉЃЎ


 ЛЦИдДДгХОэЯЕСаД№АИ
ЛЦИдДДгХОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЫцзХОМУЕФПьЫйЗЂеЙЃЌЛЗОГЮЪЬтдНРДдНЪмЕНШЫУЧЕФЙизЂЃЌФГаЃбЇЩњЛсЮЊСЫНтНкФмМѕХХЁЂРЌЛјЗжРржЊЪЖ
ЕФЦеМАЧщПіЃЌЫцЛњЕїВщСЫВПЗжбЇЩњЃЌЕїВщНсЙћЗжЮЊЁАЗЧГЃСЫНтЁБЁАСЫНтЁБЁАСЫНтНЯЩйЁБЁАВЛСЫНтЁБЫФРрЃЌ
ВЂНЋМьВщНсЙћЛцжЦГЩЯТУцСНИіЭГМЦЭМЃЎ
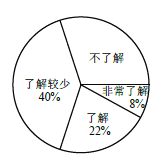
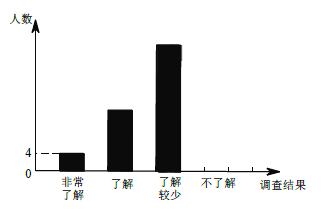
ЃЈ1ЃЉБОДЮЕїВщЕФбЇЩњЙВга__________ШЫЃЌЙРМЦИУаЃ1200 УћбЇЩњжаЁАВЛСЫНтЁБЕФШЫЪ§ЪЧ__________ШЫЃЎ
ЃЈ2ЃЉЁАЗЧГЃСЫНтЁБЕФ4 ШЫга![]() СНУћФаЩњЃЌ
СНУћФаЩњЃЌ![]() СНУћХЎЩњЃЌШєДгжаЫцЛњГщШЁСНШЫЯђШЋаЃзіЛЗБЃНЛСїЃЌЧыРћгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓЧЁКУГщЕНвЛФавЛХЎЕФИХТЪЃЎ
СНУћХЎЩњЃЌШєДгжаЫцЛњГщШЁСНШЫЯђШЋаЃзіЛЗБЃНЛСїЃЌЧыРћгУЛЪїзДЭМЛђСаБэЕФЗНЗЈЃЌЧѓЧЁКУГщЕНвЛФавЛХЎЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
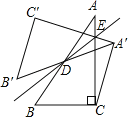
ЁОЬтФПЁПШчЭМЃЌЕуDЪЧRtЁїABCаББпABЕФжаЕуЃЌЕуEдкБпACЩЯЃЎЁїA'BЁфCЁфгыЁїABCЙигкжБЯпBEЖдГЦЃЌСЌНсAЁфCЃЎЧвЁЯCAЁфC'ЃН90ЁуЃЎШєACЃН4ЃЌBCЃН3ЃЎдђAEЕФГЄЮЊ_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌГЄЁЂПэОљЮЊ3ЃЌИпЮЊ8ЕФГЄЗНЬхШнЦїЃЌЗХжУдкЫЎЦНзРУцЩЯЃЌРяУцЪЂгаЫЎЃЌЫЎУцИпЮЊ6ЃЌШЦЕзУцвЛРтГЄНјааа§зЊЧуаБКѓЃЌЫЎУцЧЁКУДЅЕНШнЦїПкБпдЕЃЌЭМ2ЪЧДЫЪБЕФЪОвтЭМЃЌдђЭМ2жаЫЎУцИпЖШЮЊЃЈ ЃЉ

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЫљЪОЃЌ![]() жаЃЌ
жаЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕу
ЃЌЕу![]() ЁЂ
ЁЂ![]() ЗжБ№дк
ЗжБ№дк![]() ЁЂ
ЁЂ![]() БпЩЯЃЌ
БпЩЯЃЌ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌШє
ЃЌШє![]() ЃЌдђЯпЖЮ
ЃЌдђЯпЖЮ![]() ЕФГЄЮЊ______ЃЎ
ЕФГЄЮЊ______ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
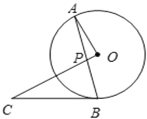
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФЯвЃЌЕуCЮЊЁбOЭтвЛЕуЃЌCOЁЭOAЃЌНЛABгкЕуPЃЌСЌНгBCЃЌBC=PCЃЎ
(1)ЧѓжЄЃКBCЪЧЁбOЕФЧаЯпЃЛ
(2)ШєЁбOЕФАыОЖЮЊ3ЃЌOP=1ЃЌЧѓPCЕФГЄЃЎ
(3)дкЃЈ2ЃЉЕФЬѕМўЯТЃЌЧѓBPЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉМЦЫуЃКЃЈ![]() Љ1ЃЉ0+2sin30Ёу-
Љ1ЃЉ0+2sin30Ёу-![]() +|Љ2017|ЃЛ
+|Љ2017|ЃЛ
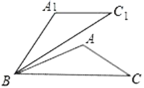
ЃЈ2ЃЉШчЭМЃЌдкЁїABCжаЃЌвбжЊЁЯABC=30ЁуЃЌНЋЁїABCШЦЕуBФцЪБеыа§зЊ50ЁуКѓЕУЕНЁїA1BC1ЃЌШєЁЯA=100ЁуЃЌЧѓжЄЃКA1C1ЁЮBCЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
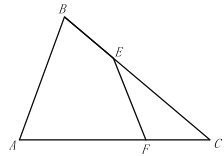
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌBCЕФДЙжБЦНЗжЯпMNНЛABгкЕуDЃЌCDЦНЗжЁЯACBЃЎШєADЃН2ЃЌBDЃН3ЃЌдђACЕФГЄЮЊ_____ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬГЁЯњЪлвЛжжЩЬЦЗЃЌШєНЋ50МўИУЩЬЦЗАДБъМлДђАЫелЯњЪлЃЌБШАДдБъМлЯњЪлетаЉЩЬЦЗЩйЛёРћ200дЊЃЎ
![]() ЧѓИУЩЬЦЗЕФБъМлЮЊЖрЩйдЊЃЛ
ЧѓИУЩЬЦЗЕФБъМлЮЊЖрЩйдЊЃЛ
![]() вбжЊИУЩЬЦЗЕФНјМлЮЊУПМў12дЊЃЌИљОнЪаГЁЕїЫЃКШєАД
вбжЊИУЩЬЦЗЕФНјМлЮЊУПМў12дЊЃЌИљОнЪаГЁЕїЫЃКШєАД![]() жаБъМлЯњЪлЃЌИУЩЬГЁУПЬьЯњЪл100МўЃЛУПеЧ1дЊЃЌУПЬьвЊЩйТє5Мў
жаБъМлЯњЪлЃЌИУЩЬГЁУПЬьЯњЪл100МўЃЛУПеЧ1дЊЃЌУПЬьвЊЩйТє5Мў![]() ФЧУДеЧМлКѓвЊЪЙИУЩЬЦЗУПЬьЕФЯњЪлРћШѓзюДѓЃЌгІНЋЯњЪлМлИёЖЈЮЊУПМўЖрЩйдЊЃПзюДѓРћШѓЪЧЖрЩйЃП
ФЧУДеЧМлКѓвЊЪЙИУЩЬЦЗУПЬьЕФЯњЪлРћШѓзюДѓЃЌгІНЋЯњЪлМлИёЖЈЮЊУПМўЖрЩйдЊЃПзюДѓРћШѓЪЧЖрЩйЃП
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com