
����Ŀ����֪������y1��ax2��2amx+am2+4��ֱ��y2��kx��km+4������a��0��a��k��m�dz�����
(1)�����ߵĶ���������______����˵��������������ֱ���Ƿ�ͬһ��(˵������)��
(2)��a��0��m=2��t��x ��t+2��y1�����ֵΪ4����t�ķ�Χ��
(3)�����ߵĶ���ΪP��ֱ���������ߵ���һ������ΪQ���������mֵ����1��k��4���߶�PQ(�������˵�)�����ٴ�������������Ϊ�����ĵ㣬��a�ķ�Χ��
���𰸡�(1)��m��4������������ֱ�߶�����ͬһ��(m��4)�����ɼ������� (2)0��t��2��(3) ![]() ����
����![]()
��������
(1)�Ȱ������߷��̻�Ϊ����ʽ���õ��������꣬�����ֱ��y2��kx��km+4����Ķ��㣬������⣻
(2) ��m=2ʱ��![]()
![]() ���ٽ��t��x ��t+2��y1�����ֵΪ4����������𰸣�
���ٽ��t��x ��t+2��y1�����ֵΪ4����������𰸣�
(3)���������ߺ�һ�κ����Ľ���ʽ���������ĺ����꣬���߶�PQ(�������˵�)�����ٴ�������������Ϊ�����ĵ��в���ʽ���㼴�ɵõ��𰸣�
�⣺(1) ��������y1��ax2��2amx+am2+4��Ϊ����ʽΪ��
![]() ��
��
�ʶ�������Ϊ(m��4)��
�֡�ֱ��y2��kx��km+4=k(x-m)+4��
��ֱ��y2��kx��km+4�����(m��4)��
����������ֱ���Ƿ�ͬһ��(m��4) ��
(2)��m=2ʱ��![]()
![]() ��
��
����a��0��
�������߿������£���x=2ʱȡ�����ֵ4��
�֡�t��x ��t+2��y1�����ֵΪ4��
��![]()
��0��t��2��
(3)��![]() ������
������![]() =kx��km+4�����
=kx��km+4�����![]() =m��
=m��![]() =m+
=m+![]() ��
��
���߶�PQ�����ٴ�������������Ϊ�����ĵ㣬k>0��
��![]() ����
����![]() ��
��
�֡�1��k��4��
��![]() ����
����![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��.��֪���ھ���![]() �У�
�У�![]() �ǶԽ��ߣ�
�ǶԽ��ߣ�![]() �ڵ�
�ڵ�![]() ��
��![]() �ڵ�
�ڵ�![]() ��
��
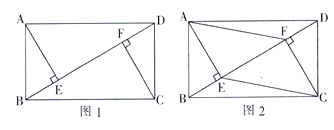
��1����ͼ1����֤��![]() ��
��
��2����ͼ2����![]() ʱ������
ʱ������![]() .
.![]() ���ڲ������κθ����ߵ�����£���ֱ��д��ͼ2���ĸ������Σ�ʹд����ÿ�������ε���������ھ���
���ڲ������κθ����ߵ�����£���ֱ��д��ͼ2���ĸ������Σ�ʹд����ÿ�������ε���������ھ���![]() �����
�����![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������ε�һ����ƽ�����뱻ƽ�ֵĽǵ�һ����ȣ�������������Ϊ������������������������ƽ���߽�����������ε�������������ͼ�٣�AD�ǡ�ABC�Ľ�ƽ���ߣ���AD��ABʱ�����ABC���������������������߶�AD�ǡ�ABC������������
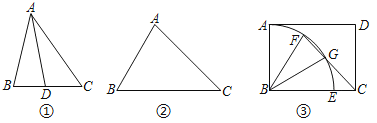
��1����ͼ�ڣ��ڡ�ABC�У���B��60������C��45������֤����ABC��������������������
��2����ͼ�ۣ��ھ���ABCD�У�AB��3��BC��4����BΪԲ���ھ����ڲ���![]() ����BC�ڵ�E����F��
����BC�ڵ�E����F��![]() ��һ�㣬����CF����CF��
��һ�㣬����CF����CF��![]() ����һ������G������BG����BG�ǡ�BCF�ġ����ߡ�ʱ����CG�ij���
����һ������G������BG����BG�ǡ�BCF�ġ����ߡ�ʱ����CG�ij���
��3����֪��ABC�ǡ������������Ρ���AD�ǡ����ߡ�����AB��3BD����AC��BC��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
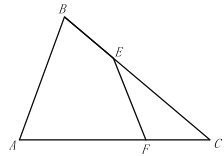
����Ŀ����ͼ��ʾ��![]() �У�
��![]() ��
��![]() ����
����![]() ��
��![]() �ֱ���
�ֱ���![]() ��
��![]() ���ϣ�
���ϣ�![]() ������
������![]() ����
����![]() �����߶�
�����߶�![]() �ij�Ϊ______��
�ij�Ϊ______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����4����ͬ�Ŀ�Ƭ������ֱ�д������1��2��3��5������Ƭϴ�Ⱥ��泯�ϣ�
(1)���������ȡ1�ţ���õĿ�Ƭ������Ϊ�����ĸ�����_______��
(2)���������ȡ1�ţ��������������Ϊʮλ������¼�����Ż����������ȡ1�Ű������������Ϊ��λ��������ɵ���λ����3�ı����ĸ��ʣ�(����״ͼ���б��ķ���)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1�����㣺��![]() ��1��0+2sin30��-
��1��0+2sin30��-![]() +|��2017|��
+|��2017|��
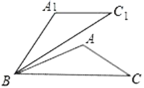
��2����ͼ������ABC�У���֪��ABC=30��������ABC�Ƶ�B��ʱ����ת50����õ���A1BC1������A=100������֤��A1C1��BC��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ��������Ƶ�ʹ��Ƹ�������ʵ��ʱ��������ijһ������ֵ�Ƶ������ͼ���������һ�����ʵ������ǣ�������
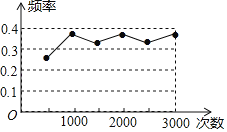
A.��һöӲ�ң��������泯��
B.�ӱ���1��2��3��4��5��6�����ſ�Ƭ���γ�һ�ţ�����ż��
C.��һ��װ��6�������3������Ĵ�������ȡһ��ȡ�����Ǻ���
D.һ��ȥ����С�����˿���ϴ�Ⱥ����γ�һ���ƵĻ�ɫ�Ǻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
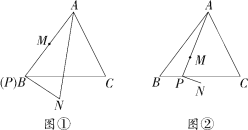
����Ŀ����ͼ���ڡ�ABC�У�AB��BC��10��tan��ABC��![]() ����P�DZ�BC�ϵ�һ�㣬M���߶�AP��һ�㣬�߶�PM�Ƶ�P˳ʱ����ת90�����߶�PN����BP��t��
����P�DZ�BC�ϵ�һ�㣬M���߶�AP��һ�㣬�߶�PM�Ƶ�P˳ʱ����ת90�����߶�PN����BP��t��
(1)��ͼ�٣�����P�ڵ�B����M��AP�е�ʱ������AN�ij���
(2)��ͼ�ڣ���![]() ��
��![]() ʱ��
ʱ��
�����N��BC�ߵľ���(�ú�t�Ĵ���ʽ��ʾ)��
�ڵ���P�ӵ�B�˶�����Cʱ�������N�˶�·���ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������EFG�У���G��90����![]() ��������ABCD�ı߳�Ϊ1����������ABCD����EFG��ͼ���ã�AD��EF��һ��ֱ���ϣ���A���E�غϣ��ֽ�������ABCD��EF������ÿ��1����λ���ٶ������˶�������A���F�غ�ʱֹͣ��������˶������У�������ABCD����EFG�ص����ֵ����S���˶�ʱ��t�ĺ���ͼ������ǣ�������
��������ABCD�ı߳�Ϊ1����������ABCD����EFG��ͼ���ã�AD��EF��һ��ֱ���ϣ���A���E�غϣ��ֽ�������ABCD��EF������ÿ��1����λ���ٶ������˶�������A���F�غ�ʱֹͣ��������˶������У�������ABCD����EFG�ص����ֵ����S���˶�ʱ��t�ĺ���ͼ������ǣ�������
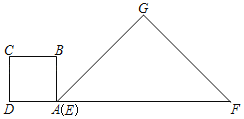
A.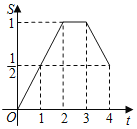 B.
B.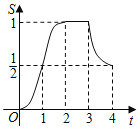
C.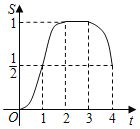 D.
D.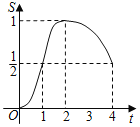
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com