
已知,AB是⊙O的直径,点P在弧AB上(不含点A、B),把△AOP沿OP对折,点A的对应点C恰好落在⊙O上.
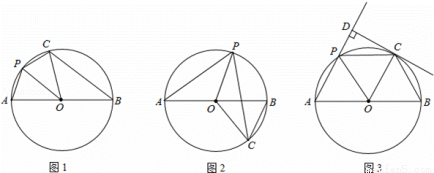
(1)当P、C都在AB上方时(如图1),判断PO与BC的位置关系(只回答结果);
(2)当P在AB上方而C在AB下方时(如图2),(1)中结论还成立吗?证明你的结论;
(3)当P、C都在AB上方时(如图3),过C点作CD⊥直线AP于D,且CD是⊙O的切线,证明:AB=4PD.
见解析
【解析】
试题分析:(1)根据图形可知PO∥BC;(2)根据图形可知PO∥BC结论仍成立,根据条件只需要证明∠CPO=∠PCB即可;(3)根据条件证得△APO为等边三角形,进而得∠OCP=60°,CD是⊙O的切线,得∠OCD=90°,所以∠DCP=30°,所以PC=2PD,PC=AP=OA,所以AB=4PD.
试题解析:【解析】
(1)PO与BC的位置关系是PO∥BC;
(2)(1)中的结论PO∥BC成立,理由为:
由折叠可知:△APO≌△CPO,
∴∠APO=∠CPO, 又∵OA=OP,
∴∠A=∠APO, ∴∠A=∠CPO,
又∵∠A与∠PCB都为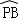 所对的圆周角,
所对的圆周角,
∴∠A=∠PCB, ∴∠CPO=∠PCB, ∴PO∥BC;
(3)∵CD为圆O的切线,
∴OC⊥CD,又AD⊥CD, ∴OC∥AD,
∴∠APO=∠COP, 由折叠可得:∠AOP=∠COP,
∴∠APO=∠AOP, 又OA=OP,∴∠A=∠APO,
∴∠A=∠APO=∠AOP, ∴△APO为等边三角形,
∴∠AOP=60°, 又∵OP∥BC,∴∠OBC=∠AOP=60°,又OC=OB,
∴△BCO为等边三角形,∴∠COB=60°,
∴∠POC=180°﹣(∠AOP+∠COB)=60°,又OP=OC,∴△POC也为等边三角形,
∴∠PCO=60°,PC=OP=OC, 又∵∠OCD=90°,∴∠PCD=30°,
在Rt△PCD中,PD=PC,
又∵PC=OP=AB,∴PD=AB,即AB=4PD.
考点:1.全等三角形的性质与判定;2.圆周角定理;3.切线的性质;4. 等边三角形的判定与性质.


科目:初中数学 来源:2014-2015学年山西省九年级10月月考数学试卷(解析版) 题型:选择题
如图,正五边形FGHMN是由正五边形ABCDE经过位似变换得到的,若AB∶FG=2∶3,则下列结论正确的是

A、2DE=3MN B、3DE=2MN
C、 D、
D、
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省东莞市南开实验学校九年级上学期期中考试数学试卷(解析版) 题型:填空题
如图,一个圆心角为90°的扇形,半径OA=2,那么图中阴影部分的面积为________(结果保留π).

查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省东莞市南开实验学校九年级上学期期中考试数学试卷(解析版) 题型:解答题
已知平面直角坐标系中三点的坐标分别为:A(4、4),B(-2,2),C(3,0)
画出它的以原点O为对称中心的△AˊBˊCˊ,写出 Aˊ,Bˊ,Cˊ三点的坐标。

查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省云浮市郁南县三八年级上学期期中联考数学试卷(解析版) 题型:选择题
在平面直角坐标系中,点P(-2,3)关于x轴的对称点在( ).
A.第一象限 B.第二象限 C.第三象限 D.第四象限
查看答案和解析>>
科目:初中数学 来源:2014-2015学年广东省云浮市郁南县三八年级上学期期中联考数学试卷(解析版) 题型:填空题
为了使一扇旧木门不变形,木工师傅在木门的背面加钉了一根木条这样做的道理是三角形具有______________.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市九年级上学期期中考试数学试卷(解析版) 题型:选择题
如图,正方形ABCD的边长为6,点E是AB上的一点,将△BCE沿CE折叠至△FCE,若CF,CE恰好与以正方形ABCD的中心为圆心的⊙O相切,则折痕CE的长为( )

A.4 B.
B.  C.
C. D.2
D.2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com