
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣2mx+n(m≠0)与x轴交于点A,B,点A的坐标为(﹣2,0).
(1)写出抛物线的对称轴;
(2)直线![]() 过点B,且与抛物线的另一个交点为C.
过点B,且与抛物线的另一个交点为C.
①分别求直线和抛物线所对应的函数表达式;
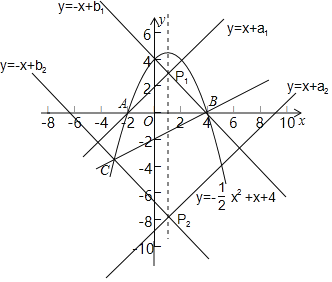
②点P为抛物线对称轴上的动点,过点P的两条直线l1:y=x+a和l2:y=﹣x+b组成图形G.当图形G与线段BC有公共点时,直接写出点P的纵坐标t的取值范围.
【答案】(1)抛物线的对称轴为直线x=1;(2)①直线所对应的函数表达式为![]() ,抛物线所对应的函数表达式为
,抛物线所对应的函数表达式为![]() ;②
;②![]()
【解析】
(1)由给定的抛物线的表达式,利用二次函数的性质即可找出抛物线的对称轴;
(2)①根据抛物线的对称性可得出点B的坐标,再利用二次函数图象上点的坐标特征及一次函数图象上点的坐标特征,即可求出m、n的值,此问得解;
②联立直线及抛物线的函数关系式成方程组,通过解方程组可求出点C的坐标,利用一次函数图象上点的坐标特征求出直线l2过点B、C时b的值,进而可得出点P的坐标,再结合函数图象即可找出当图形G与线段BC有公共点时,点P的纵坐标t的取值范围.
(1)∵抛物线所对应的函数表达式为y=mx2﹣2mx+n,
∴抛物线的对称轴为直线x=﹣![]() =1.
=1.
(2)①∵抛物线是轴对称图形,
∴点A、B关于直线x=1对称.
∵点A的坐标为(﹣2,0),
∴点B的坐标为(4,0).
∵抛物线y=mx2﹣2mx+n过点B,直线y=![]() x﹣4m﹣n过点B,
x﹣4m﹣n过点B,
∴![]() ,
,
解得: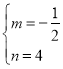 ,
,
∴直线所对应的函数表达式为![]() ,抛物线所对应的函数表达式为
,抛物线所对应的函数表达式为![]() .
.
②联立两函数表达式成方程组,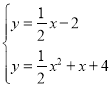 ,
,
解得: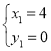 ,
, .
.
∵点B的坐标为(4,0),
∴点C的坐标为(﹣3,﹣![]() ).
).
当直线l2:y=﹣x+b1过点B时,0=﹣4+b1,
解得:b1=4,
∴此时直线l2所对应的函数表达式为y=﹣x+4,
当x=1时,y=﹣x+4=3,
∴点P1的坐标为(1,3);
当直线l2:y=﹣x+b2过点C时,﹣![]() =3+b2,
=3+b2,
解得:b2=﹣![]() ,
,
∴此时直线l2所对应的函数表达式为y=﹣x﹣![]() ,
,
当x=1时,y=﹣x﹣![]() =﹣
=﹣![]() ,
,
∴点P2的坐标为(1,﹣![]() ).
).
∴当图形G与线段BC有公共点时,点P的纵坐标t的取值范围为![]()


科目:初中数学 来源: 题型:
【题目】如图,对称轴为直线![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() 连接
连接![]() 其中
其中![]() 点坐标
点坐标![]() .
.
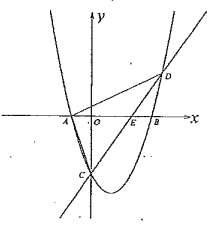
(1)求抛物线的解析式;
(2)直线![]() 与抛物线交于点
与抛物线交于点![]() 与
与![]() 轴交于点
轴交于点![]() 求
求![]() 的面积;
的面积;
(3)在直线![]() 下方抛物线上有一点
下方抛物线上有一点![]() 过
过![]() 作
作![]() 轴交直线
轴交直线![]() 于点
于点![]() .四边形
.四边形![]() 为平行四边形,求点
为平行四边形,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,帆船A和帆船B在太湖湖面上训练,O为湖面上的一个定点,教练船静候于O点,训练时要求A、B两船始终关于O点对称.以O为原点,建立如图所示的坐标系,x轴、y轴的正方向分别表示正东、正北方向.设A、B两船可近似看成在双曲线y=![]() 上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).
上运动,湖面风平浪静,双帆远影优美,训练中当教练船与A、B两船恰好在直线y=x上时,三船同时发现湖面上有一遇险的C船,此时教练船测得C船在东南45°方向上,A船测得AC与AB的夹角为60°,B船也同时测得C船的位置(假设C船位置不再改变,A、B、C三船可分别用A、B、C三点表示).

(1)发现C船时,A、B、C三船所在位置的坐标分别为A(_______,_______)、B(_______,_______)和C(_______,_______);
(2)发现C船,三船立即停止训练,并分别从A、O、B三点出发沿最短路线同时前往救援,设A、B两船的速度相等,教练船与A船的速度之比为3:4,问教练船是否最先赶到?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,抛物线yax24axc的图象经过点A0,4.
(1)请直接写出抛物线的对称轴的表达式 .
(2)已知点B(1,4a),点C在直线AB上,且点C的横坐标为4,请直接写出点C的纵坐标(用含a的式子表示) .
(3)在(2)的条件下,抛物线的图象与线段BC恰有一个公共点,请直接写出a的取值范围 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】党的十八大提出,倡导富强、民主、文明、和谐,倡导自由、平等、公正、法治,倡导爱国、敬业、诚信、友善,积极培育和践行社会主义核心价值观,这24个字是社会主义核心价值观的基本内容.其中:
“富强、民主、文明、和谐”是国家层面的价值目标;
“自由、平等、公正、法治”是社会层面的价值取向;
“爱国、敬业、诚信、友善”是公民个人层面的价值准则.

小光同学将其中的“文明”、“和谐”、“自由”、“平等”的文字分别贴在4张硬纸板上,制成如右图所示的卡片.将这4张卡片背面朝上洗匀后放在桌子上,从中随机抽取一张卡片,不放回,再随机抽取一张卡片.
(1)小光第一次抽取的卡片上的文字是国家层面价值目标的概率是 ;
(2)请你用列表法或画树状图法,帮助小光求出两次抽取卡片上的文字一次是国家层面价值目标、一次
是社会层面价值取向的概率(卡片名称可用字母表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了加强学校的体育活动,某学校计划购进甲、乙两种篮球,根据市场调研发现,如果购进甲篮球2个和乙篮球3个共需270元;购进甲篮球3个和乙篮球2个共需230元.
(1)求甲、乙两种篮球每个的售价分别是多少元?
(2)为满足开展体育活动的需求,学校计划购进甲、乙两种篮球共100个,由于购货量大,和商场协商,商场决定甲篮球以九折出售,乙篮球以八折出售,学校要求甲种篮球的数量不少于乙种篮球数量的4倍,甲种篮球的数量不多于90个,请你求出学校花最少钱的进货方案;
(3)学校又拿出省下的290元购买跳绳和毽子两种体育器材,跳绳10元一根,毽子5元一个,在把钱用尽的情况下,有多少种进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,ABCD的对角线AC、BD相交于点O,∠BDC=45°,过点B作BH⊥DC交DC的延长线于点H,在DC上取DE=CH,延长BH至F,使FH=CH,连接DF、EF.

(1)若AB=2,AD=![]() ,求BH的值;
,求BH的值;
(2)求证:AC=![]() EF.
EF.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com