
【题目】数学兴趣小组的同学们对函数 的图象和性质进行了探究,已知
的图象和性质进行了探究,已知![]() 时,函数
时,函数![]() 的图象的对称轴为直线
的图象的对称轴为直线![]() ,顶点在
,顶点在![]() 轴上,与
轴上,与![]() 轴的交点坐标为
轴的交点坐标为![]() ,探究过程如下,请补充过程:
,探究过程如下,请补充过程:
(1)![]() ,
,![]() ,
,![]() .
.
(2)在给出的平面直角坐标系中,画出函数图象,并写出这个函数的一条性质: .
(3)进一步探究函数图象并解决问题:
①若![]() 有三个实数解,则
有三个实数解,则![]() 的取值范围为: .
的取值范围为: .
②若函数![]() 的图象与该函数有三个交点,则
的图象与该函数有三个交点,则![]() 的取值范围为: .
的取值范围为: .
【答案】(1)![]() ,
,![]() ,
,![]() ;(2)图详见解析;性质不唯一,详见解析;(3)①
;(2)图详见解析;性质不唯一,详见解析;(3)①![]() ;②
;②![]()
【解析】
(1)根据函数![]() 的图象的对称轴为直线
的图象的对称轴为直线![]() ,顶点在
,顶点在![]() 轴上,与
轴上,与![]() 轴的交点坐标为
轴的交点坐标为![]() ,得到关于a,b,c的方程组,解方程即可;
,得到关于a,b,c的方程组,解方程即可;
(2)根据题意,分别画出当x≤1,x>1,时两部分的图像,并结合图像任意写出一条性质即可;
(3)①根据函数图像,画出![]() ,根据图像确定即可;
,根据图像确定即可;
②![]() 与该函数有三个交点,根据函数图象,当
与该函数有三个交点,根据函数图象,当![]() 的图象经过点
的图象经过点![]() 时,此时
时,此时![]() 最大,为
最大,为![]() ;当
;当![]() 的图象与二次函数的图象相切时,此为另一种临界情况,直线与图像有两个交点,联立方程组,
的图象与二次函数的图象相切时,此为另一种临界情况,直线与图像有两个交点,联立方程组,![]() ,求出n,问题得解.
,求出n,问题得解.
解:(1)由题意得![]() 的图象对称轴为直线
的图象对称轴为直线![]() ,经过
,经过![]() ,
,![]()
则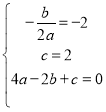 ,解得
,解得![]()
∴![]() ,
,![]() ,
,![]()
(2)函数图像如图:
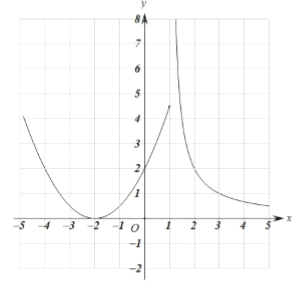
性质:当![]() 时,
时,![]() 随
随![]() 的增大而减小;
的增大而减小;
当![]() 时,
时,![]() 随
随![]() 的增大而增大;
的增大而增大;
当![]() 时,
时,![]() 随
随![]() 的增大而减小.
的增大而减小.
当![]() 时,函数有最小值为0;
时,函数有最小值为0;
(3)①![]() 有三个解,即函数图像与直线
有三个解,即函数图像与直线![]() 有三个交点
有三个交点
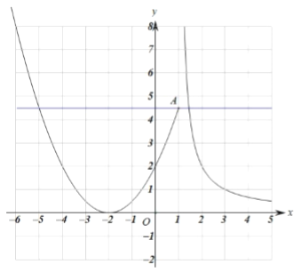
![]() ,当直线
,当直线![]() 为直线
为直线![]() 或在其下方且在
或在其下方且在![]() 轴上方时,与函数图象有三个交点,
轴上方时,与函数图象有三个交点,
因此:![]()
②
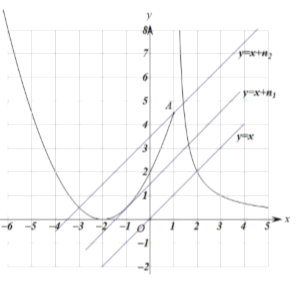
![]() 与该函数有三个交点,根据函数图象,
与该函数有三个交点,根据函数图象,
当![]() 的图象经过点
的图象经过点![]() 时,此时
时,此时![]() 最大,为
最大,为![]() ;
;
当![]() 的图象与二次函数的图象相切时,此为另一种临界情况.
的图象与二次函数的图象相切时,此为另一种临界情况.
联立解析式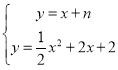 ,
,
得![]() ,由
,由![]() ,得
,得![]() ,
,
因此:![]() .
.


科目:初中数学 来源: 题型:
【题目】如图1,给定一个正方形,要通过画线将其分割成若干个互不重叠的正方形.第1次画线分割成4个互不重叠的正方形,得到图2;第2次画线分割成7个互不重叠的正方形,得到图3……以后每次只在上次得到图形的左上角的正方形中画线.
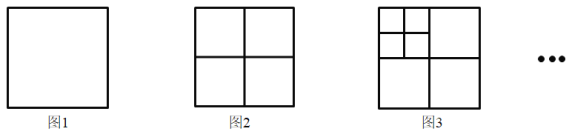
尝试:第3次画线后,分割成 个互不重叠的正方形;
第4次画线后,分割成 个互不重叠的正方形.
发现:第n次画线后,分割成 个互不重叠的正方形;并求第2020次画线后得到互不重叠的正方形的个数.
探究:若干次画线后,能否得到1001个互不重叠的正方形?若能,求出是第几次画线后得到的;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年11月22日,教育部发布关于《中小学教师实施教育惩戒规则(征求意见稿)》公开征求意见的通知,征求意见稿指出;教育惩戒是教师履行救育教学职责的必要手段和法定职权.教育惩戒分为![]() :一般惩戒,
:一般惩戒,![]() :较重惩戒,
:较重惩戒,![]() :严重惩戒,
:严重惩戒,![]() :强制措施,共四个层次.为了解家长对教育惩戒的看法,某中学对学生家长进行了随机调查,要求每位家长选择其中最关注的一个层次提出意见,学校对收集的信息进行统计,绘制了下面两幅不完整的统计图.
:强制措施,共四个层次.为了解家长对教育惩戒的看法,某中学对学生家长进行了随机调查,要求每位家长选择其中最关注的一个层次提出意见,学校对收集的信息进行统计,绘制了下面两幅不完整的统计图.

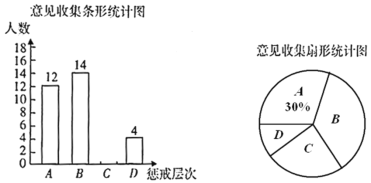
请你根据统计图提供的信息,解答下列问题:
(1)被调查的总人数是______人;
(2)扇形统计图中![]() 部分对应的圆心角的度数为______;
部分对应的圆心角的度数为______;
(3)补全条形统计图;
(4)某班主任对学生进行了纪律教育,要求小明和小军分别从题中所述的四个层次中随机选择一个层次说明惩戒内容.请用列表法或画树状图法求两人选择不同教育惩戒层次的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数![]() 的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )
的图象沿y轴向上平移得到一条新函数的图象,其中点A(-4,m),B(-1,n),平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是 ( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
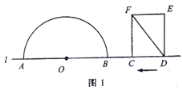
【题目】如图1,点![]() 和矩形
和矩形![]() 的边
的边![]() 都在直线
都在直线![]() 上,以点
上,以点![]() 为圆心,以24为半径作半圆,分别交直线
为圆心,以24为半径作半圆,分别交直线![]() 于
于![]() 两点.已知:
两点.已知: ![]() ,
,![]() ,矩形自右向左在直线
,矩形自右向左在直线![]() 上平移,当点
上平移,当点![]() 到达点
到达点![]() 时,矩形停止运动.在平移过程中,设矩形对角线
时,矩形停止运动.在平移过程中,设矩形对角线![]() 与半圆
与半圆![]() 的交点为
的交点为![]() (点
(点![]() 为半圆上远离点
为半圆上远离点![]() 的交点).
的交点).
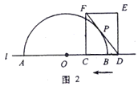
(1)如图2,若![]() 与半圆
与半圆![]() 相切,求
相切,求![]() 的值;
的值;
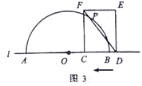
(2)如图3,当![]() 与半圆
与半圆![]() 有两个交点时,求线段
有两个交点时,求线段![]() 的取值范围;
的取值范围;
(3)若线段![]() 的长为20,直接写出此时
的长为20,直接写出此时![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长都是1的小正方形组成的网格中,![]() 均为格点,线段
均为格点,线段![]() ,
,![]() 相交于点
相交于点![]() .
.

(1)![]() ________;
________;
(2)设![]() ,将线段
,将线段![]() 绕点
绕点![]() 逆时针旋转
逆时针旋转![]() 的角,点
的角,点![]() 的对应点为
的对应点为![]() ,请你借助网格,使用无刻度的直尺画出点
,请你借助网格,使用无刻度的直尺画出点![]() ,并简要说明你是怎么画的___________.
,并简要说明你是怎么画的___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 与x轴相交于不同的两点
与x轴相交于不同的两点![]() ,
,
(1)求![]() 的取值范围
的取值范围
(2)证明该抛物线一定经过非坐标轴上的一点![]() ,并求出点
,并求出点![]() 的坐标;
的坐标;
(3)当![]() 时,由(2)求出的点
时,由(2)求出的点![]() 和点
和点![]() 构成的
构成的![]() 的面积是否有最值,若有,求出最值及相对应的
的面积是否有最值,若有,求出最值及相对应的![]() 值;若没有,请说明理由.
值;若没有,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
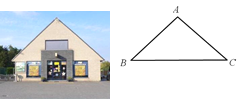
【题目】等腰三角形的屋顶,是建筑中经常采用的结构形式.在如图所示的等腰三角形屋顶ABC中,AB=AC,测得BC=20米,∠C=41°,求顶点A到BC边的距离是多少米?(结果精确到0.1米.参考数据:sin41°≈0.656,cos41°≈0.755,tan41°≈0.869.)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”“10元”“20元”“30元”的字样.规定:顾客在本超市一次性消费满200元,就可以在箱子里先后摸出2个小球(第一次摸出后不放回).某顾客刚好消费200元,则该顾客所获得购物券的金额不低于30元的概率是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com