
| A. | H有最大值20 | B. | H有最小值6 | C. | G有最小值6 | D. | G有最大值20 |
分析 首先求出两函数交点坐标,进而利用函数图象得出交点,即可得出H的最小值.
解答 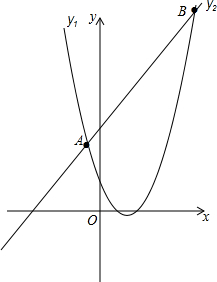 解:y1=(x-$\frac{3}{2}$)2-$\frac{1}{4}$,y1的图象是顶点为($\frac{3}{2}$,-$\frac{1}{4}$),
解:y1=(x-$\frac{3}{2}$)2-$\frac{1}{4}$,y1的图象是顶点为($\frac{3}{2}$,-$\frac{1}{4}$),
对称轴为x=$\frac{3}{2}$,开口向上的抛物线,
解方程组$\left\{\begin{array}{l}{y=2x+8}\\{y={x}^{2}-3x+2}\end{array}\right.$,
得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=6}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=6}\\{{y}_{2}=20}\end{array}\right.$,
即函数y1与y2的图象的交点为(-1,6),(6,20),
函数max{y1,y2}的图象如图所示,当x=-1时,y1=y2=6,
故H有最小值6.
故选:B.
点评 此题主要考查了二次函数最值以及一次函数与二次函数交点坐标求法,利用数形结合得出是解题关键.


 王后雄学案教材完全解读系列答案
王后雄学案教材完全解读系列答案 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
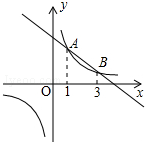 如图,在平面直角坐标系中,反比例函数y1=$\frac{3}{x}$的图象与一次函数y2=kx+b的图象交于A、B两点.若y1<y2,则x的取值范围是( )
如图,在平面直角坐标系中,反比例函数y1=$\frac{3}{x}$的图象与一次函数y2=kx+b的图象交于A、B两点.若y1<y2,则x的取值范围是( )| A. | 1<x<3 | B. | x<0或1<x<3 | C. | 0<x<1 | D. | x>3或0<x<1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com