
【题目】如图,顶点为![]() 的抛物线
的抛物线![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于点
轴交于点![]() ,过点
,过点![]() 作
作![]() 轴交抛物线于另一点
轴交抛物线于另一点![]() ,作
,作![]() 轴,垂足为点
轴,垂足为点![]() .双曲线
.双曲线![]() 经过点
经过点![]() ,连接
,连接![]() ,
,![]() .
.
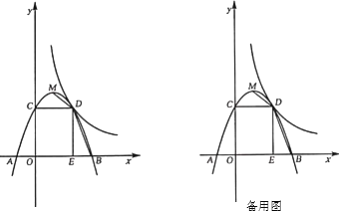
(1)求抛物线的表达式;
(2)点![]() ,
,![]() 分别是
分别是![]() 轴,
轴,![]() 轴上的两点,当以
轴上的两点,当以![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形周长最小时,求出点
为顶点的四边形周长最小时,求出点![]() ,
,![]() 的坐标;
的坐标;
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,以点(3,-5)为圆心,r为半径的圆上有且仅有两点到x轴所在直线的距离等于1,则圆的半径r的取值范围是 ( )
A.r>4 B.0<r<6 C.4≤r<6 D.4<r<6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴交于A(﹣1,0)B(3,0)两点,与y轴交于点C.
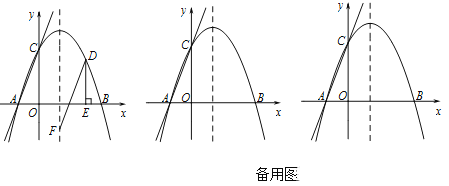
(1)求抛物线y=ax2+2x+c的解析式:;
(2)点D为抛物线上对称轴右侧、x轴上方一点,DE⊥x轴于点E,DF∥AC交抛物线对称轴于点F,求DE+DF的最大值;
(3)①在拋物线上是否存在点P,使以点A,P,C为顶点,AC为直角边的三角形是直角三角形?若存在,请求出符合条件的点P的坐标;若不存在,请说明理由;
②点Q在抛物线对称轴上,其纵坐标为t,请直接写出△ACQ为锐角三角形时t的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
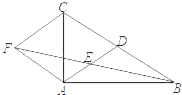
【题目】如图,在△ABC中,AD是BC边上的中线,点E是AD的中点,连接BE,过点A作BC的平行线交BE的延长线于点F,连接CF.
(1)求证:AF=DC;
(2)在不添加任何辅助线的情况下,请直接写出图中四个三角形,使写出的每个三角形的面积等于△AEF面积的2倍.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=-x2+1,下列结论:
①抛物线开口向上;
②抛物线与x轴交于点(-1,0)和点(1,0);
③抛物线的对称轴是y轴;
④抛物线的顶点坐标是(0,1);
⑤抛物线y=-x2+1是由抛物线y=-x2向上平移1个单位得到的.
其中正确的个数有( )
A. 5个B. 4个C. 3个
D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】十八大以来,某校已举办五届校园艺术节.为了弘扬中华优秀传统文化,每届艺术节上都有一些班级表演“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”等节目.小颖对每届艺术节表演这些节目的班级数进行统计,并绘制了如图所示不完整的折线统计图和扇形统计图.
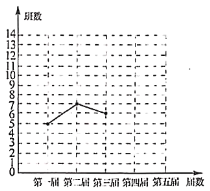
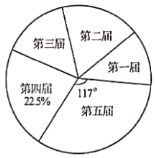
(1)五届艺术节共有________个班级表演这些节日,班数的中位数为________,在扇形统计图中,第四届班级数的扇形圆心角的度数为________;
(2)补全折线统计图;
(3)第六届艺术节,某班决定从这四项艺术形式中任选两项表演(“经典诵读”、“民乐演奏”、“歌曲联唱”、“民族舞蹈”分别用![]() ,
,![]() ,
,![]() ,
,![]() 表示).利用树状图或表格求出该班选择
表示).利用树状图或表格求出该班选择![]() 和
和![]() 两项的概率.
两项的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有10个人围成一个圆圈做游戏.游戏的规则是:每个人心里都想好一个数,并把自己想好的数如实地告诉他两旁的两个人,然后每个人将他两旁的两个人告诉他的数的平均数报出来.若报出来的数如图所示,则报3的人心里想的数是____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线的顶点为A(1,4),抛物线与y轴交于点B(0,3),与x轴交于C,D两点.点P是x轴上的一个动点.
(1)求此抛物线的解析式;
(2)当PA+PB的值最小时,求点P的坐标;
(3)抛物线上是否存在一点Q(Q与B不重合),使△CDQ的面积等于△BCD的面积?若存在,直接写出点Q的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
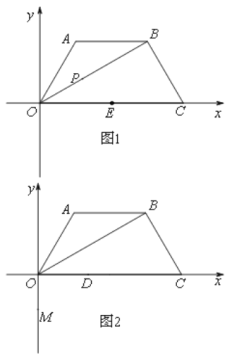
【题目】如图1,等腰梯形OABC的底边OC在x轴上,AB∥OC,O为坐标原点,OA = AB =BC,∠AOC=60°,连接OB,点P为线段OB上一个动点,点E为边OC中点.
(1)连接PA.PE,求证:PA=PE;
(2)连接PC,若PC+PE=2![]() ,试求AB的最大值;
,试求AB的最大值;
(3)在(2)在条件下,当AB取最大值时,如图2,点M坐标为(0,-1),点D为线段OC上一个动点,当D点从O点向C点移动时,直线MD与梯形另一边交点为N,设D点横坐标为m,当△MNC为钝角三角形时,求m的范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com