
【题目】根据下列证明过程填空,请在括号里面填写对应的推理的理由.如图,已知:直线AB、CD被直线BC所截;直线BC、DE被直线CD所截,∠1+∠2 =180°,且∠1=∠D,求证:BC∥DE.
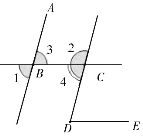
证明:∵∠1+∠2=180°(已知)
又∵∠1=∠3 .
∴∠2+∠3=180°(等量代换)
∴AB∥ .
∴∠4=∠1 .
又∵∠1=∠D .
∴∠D= (等量代换)
∴BC∥DE( ).
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:初中数学 来源: 题型:
【题目】规定:如果两个一次函数的一次项系数和常数项互换,即y=kx+b和y=bx+k(其中|k|≠|b|),称这样的两个一次函数为互助一次函数,例如![]() 和
和![]() 就是互助一次函数.根据规定解答下列问题:
就是互助一次函数.根据规定解答下列问题:
(1)填空:一次函数![]() 与它的互助一次函数的交点坐标为______
与它的互助一次函数的交点坐标为______
(2)若两个一次函数y=(k-b)x – k - 2b与![]() 是互助一次函数,求两函数图象与y轴围成的三角形的面积.
是互助一次函数,求两函数图象与y轴围成的三角形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
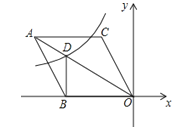
【题目】如图,在平面直角坐标系中,菱形ABOC的顶点O在坐标原点,边BO在x轴的负半轴上,∠BOC=60°,顶点C的坐标为(m,![]() ),反比例函数
),反比例函数![]() 的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
的图像与菱形对角线AO交于D点,连接BD,当BD⊥x轴时,k的值是( )
A. ![]() B. -
B. -![]() C.
C. ![]() D. -
D. -![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
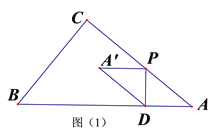
【题目】如图(1),在△ABC中,∠C=90°,AB=5cm,BC=3cm,动点P在线段AC上以5cm/s的速度从点A运动到点C,过点P作PD⊥AB于点D,将△APD绕PD的中点旋转180°得到△A′DP,设点P的运动时间为x(s).
(1)当点A′落在边BC上时,求x的值;
(2)在动点P从点A运动到点C过程中,当x为何值时,△A′BC是以A′B为腰的等腰三角形;
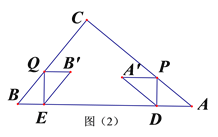
(3)如图(2),另有一动点Q与点P同时出发,在线段BC上以5cm/s的速度从点B运动到点C,过点Q作QE⊥AB于点E,将△BQE绕QE的中点旋转180°得到△B′EQ,连结A′B′,当直线A′B′与△ABC的一边垂直时,求线段A′B′的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图1,AB∥CD,∠A=35°,∠C=40°,求∠APC的度数.(提示:作PE∥AB).
(2)如图2,AB∥DC,当点P在线段BD上运动时,∠BAP=∠α,∠DCP=∠β,求∠CPA与∠α,∠β之间的数量关系,并说明理由.
(3)在(2)的条件下,如果点P在射线DM上运动,请你直接写出∠CPA与∠α,∠β之间的数量关系______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果批发商场销售一种高档水果,如果每千克盈利10元,每天可售出500千克,经市场调查发现,在进货价不变的情况下.若每千克涨价1元,日销售量将减少20千克.
(1)现该商场要保证每天盈利6000元,同时又要使顾客得到实惠,那么每千克应涨价多少元?
(2)每千克水果涨价多少元时,商场每天获得的利润最大?获得的最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线y=3x﹣3分别交x轴、y轴于A、B两点,抛物线y=x2+bx+c经过A、B两点,点C是抛物线与x轴的另一个交点(与A点不重合).
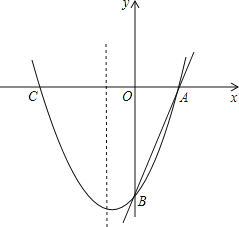
(1)求抛物线的解析式;
(2)求△ABC的面积;
(3)在抛物线的对称轴上,是否存在点M,使△ABM为等腰三角形?若不存在,请说明理由;若存在,求出点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了推动我县“三进校园”活动的广泛开展,引导学生走向操场,走到阳光下,积极参加体育锻炼,学校准备购买一批运动鞋供学生借用,现从各年级随机抽取了部分学生的鞋号,绘制了如下的统计图①和图②,请根据相关信息,解答下列问题:

(1)本次接受随机抽样调查的学生人数为 ,图①中![]() 的值为 ;
的值为 ;
(2)本次调查获取的样本数据的众数为 ,中位数为 ;
(3)根据样本数据,若学校计划购买![]() 双运动鞋,建议购买
双运动鞋,建议购买![]() 号运动鞋 双.
号运动鞋 双.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com