
【题目】如图,抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴于
轴于![]() 点,点
点,点![]() 的坐标为
的坐标为![]() ,直线
,直线![]() 经过点
经过点![]() .
.

(1)求抛物线的函数表达式;
(2)点![]() 是直线
是直线![]() 上方抛物线上的一动点,求
上方抛物线上的一动点,求![]() 面积
面积![]() 的最大值并求出此时点
的最大值并求出此时点![]() 的坐标;
的坐标;
(3)过点![]() 的直线交直线
的直线交直线![]() 于点
于点![]() ,连接
,连接![]() 当直线
当直线![]() 与直线
与直线![]() 的一个夹角等于
的一个夹角等于![]() 的2倍时,请直接写出点
的2倍时,请直接写出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)当
;(2)当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() ,点
,点![]() 坐标为
坐标为![]() ;(3)点
;(3)点![]() 的坐标
的坐标![]() 或
或![]() .
.
【解析】
(1)利用点B的坐标,用待定系数法即可求出抛物线的函数表达式;
(2)如图1,过点P作![]() 轴,交BC于点H,设
轴,交BC于点H,设![]() ,H
,H![]() ,求出
,求出![]() 的面积即可求解;
的面积即可求解;
(3)如图2,作AN⊥BC于N,NH⊥x轴于H,作AC的垂直平分线交BC于![]() ,交AC于E,利用等腰三角形的性质和三角形外角性质得到
,交AC于E,利用等腰三角形的性质和三角形外角性质得到![]() ,再确定N(3,2),AC的解析式为y=5x5,E点坐标为
,再确定N(3,2),AC的解析式为y=5x5,E点坐标为![]() ,利用两直线垂直的问题可设直线
,利用两直线垂直的问题可设直线![]() 的解析式为
的解析式为![]() ,把E
,把E![]() 代入求出b,得到直线
代入求出b,得到直线![]() 的解析式为
的解析式为![]() ,则解方程组
,则解方程组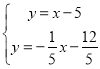 得
得![]() 点的坐标;作点
点的坐标;作点![]() 关于N点的对称点
关于N点的对称点![]() ,利用对称性得到
,利用对称性得到![]() ,设
,设![]() ,根据中点坐标公式得到
,根据中点坐标公式得到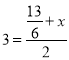 ,然后求出x即可得到
,然后求出x即可得到![]() 的坐标,从而得到满足条件的点M的坐标.
的坐标,从而得到满足条件的点M的坐标.
(1)把![]() 代入
代入![]() 得
得
![]()
![]()
![]() ;
;
(2)过点P作![]() 轴,交BC于点H,
轴,交BC于点H,

设![]() ,则点H的坐标为
,则点H的坐标为![]() ,
,
∴![]() ,
,
∴ ,
,![]()
∴当![]() 时,
时,![]() 有最大值,最大值为
有最大值,最大值为![]() ,此时点
,此时点![]() 坐标为
坐标为![]() .
.
(3)作AN⊥BC于N,NH⊥x轴于H,作AC的垂直平分线交BC于![]() ,交AC于E,
,交AC于E,
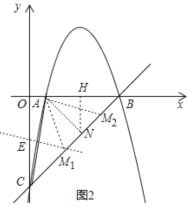
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵△ANB为等腰直角三角形,
∴![]() ,
,
∴N(3,2),
由![]() 可得AC的解析式为y=5x5,E点坐标为
可得AC的解析式为y=5x5,E点坐标为![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,把E
,把E![]() 代入得
代入得![]() ,解得
,解得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
解方程组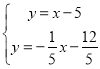 得
得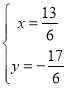 ,则
,则![]() ;
;
如图2,在直线BC上作点![]() 关于N点的对称点
关于N点的对称点![]() ,则
,则![]() ,
,
设![]() ,
,
∵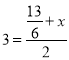 ,
,
∴![]() ,
,
∴![]() ,
,
综上所述,点M的坐标为![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,点
,点![]() 是
是![]() 边上的动点(不与
边上的动点(不与![]() 重合),点
重合),点![]() 在
在![]() 边上,并且满足
边上,并且满足![]() .
.
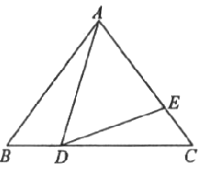
(1)求证:![]() ;
;
(2)若![]() 的长为
的长为![]() ,请用含
,请用含![]() 的代数式表示
的代数式表示![]() 的长;
的长;
(3)当(2)中的![]() 最短时,求
最短时,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O为等边△ABC的外接圆,AD∥BC,∠ADC=90°,CD交⊙O于点E.
(1)求证:AD是⊙O的切线;
(2)若DE=2,求阴影部分的面积.
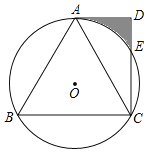
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某县建档立卡贫困户对精准扶贫政策落实的满意度,现从全县建档立卡贫困户中随机抽取了部分贫困户进行了调查(把调查结果分为四个等级:A级:非常满意:B级满意;C级:基本满意:D级:不满意),并将调查结果绘制成如两幅不完整的统计图,请根据统计图中的信息解决下列问题:
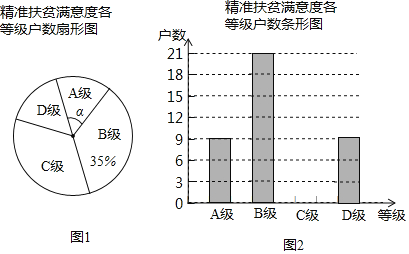
(1)本次抽样调查测试的建档立卡贫困户的总户数是 ;
(2)图①中,∠α的度数是 ,并把图②条形统计图补充完整;
(3)某县建档立卡贫困户有10000户,如果全部参加这次满意度调查,请估计非常满意的户数约为多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
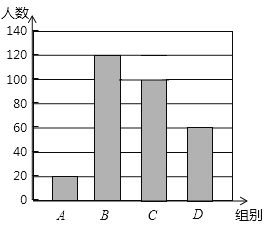
【题目】国家规定,中、小学生每天在校体育活动时间不低于1h.为此,某区就“你每天在校体育活动时间是多少”的问题随机调查了辖区内300名初中学生.根据调查结果绘制成的统计图如图所示,其中A组为t<0.5h,B组为0.5h≤t<1h,C组为1h≤t<1.5h,D组为t≥1.5h.
请根据上述信息解答下列问题:
(1)本次调查数据的众数落在 组内,中位数落在 组内;
(2)该辖区约有18000名初中学生,请你估计其中达到国家规定体育活动时间的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
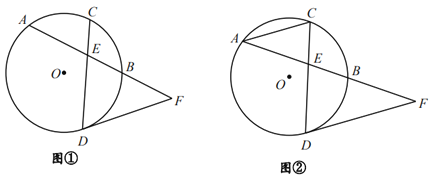
【题目】如图,已知,⊙O的半径![]() ,弦AB,CD交于点E,C为
,弦AB,CD交于点E,C为![]() 的中点,过D点的直线交AB延长线与点F,且DF=EF.
的中点,过D点的直线交AB延长线与点F,且DF=EF.
(1)如图①,试判断DF与⊙O的位置关系,并说明理由;
(2)如图②,连接AC,若AC∥DF,BE=![]() AE,求CE的长.
AE,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
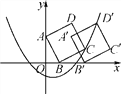
【题目】如图,在平面直角坐标系中,正方形ABCD的顶点A、B的坐标分别为(0,2)、(1,0),顶点C在函数y=![]() x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为 ______.
x2+bx-1的图象上,将正方形ABCD沿x轴正方向平移后得到正方形A′B′C′D′,点D的对应点D′落在抛物线上,则点D与其对应点D′之间的距离为 ______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系![]() 中,以
中,以![]() 为圆心作⊙
为圆心作⊙![]() ,⊙
,⊙![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,
,![]() 为⊙
为⊙![]() 上不同于
上不同于![]() 、
、![]() 的任意一点,连接
的任意一点,连接![]() 、
、![]() ,过
,过![]() 点分别作
点分别作![]() 于
于![]() ,
,![]() 于
于![]() .设点
.设点![]() 的横坐标为
的横坐标为![]() ,
,![]() .当
.当![]() 点在⊙
点在⊙![]() 上顺时针从点
上顺时针从点![]() 运动到点
运动到点![]() 的过程中,下列图象中能表示
的过程中,下列图象中能表示![]() 与
与![]() 的函数关系的部分图象是( )
的函数关系的部分图象是( )

A.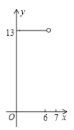 B.
B.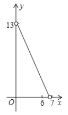 C.
C.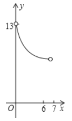 D.
D.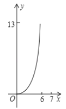
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为响应全民阅读活动,利用节假日面向社会开放学校图书馆.据统计,第一个月进馆128人次,进馆人次逐月增加,到第三个月进馆达到288人次,若进馆人次的月平均增长率相同.
(1)求进馆人次的月平均增长率;
(2)因条件限制,学校图书馆每月接纳能力不得超过500人次,在进馆人次的月平均增长率不变的条件下,校图书馆能否接待第四个月的进馆人次,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com